Page 178 - DCAP402_DCAO204_DATABASE MANAGEMENT SYSTEM_MANAGING DATABASE

Unit 10: Datalog and Recursion

10.3 Recursive Queries and Negation Notes

Consider the following rule:
Big(Part) :- Assembly(Part, Subpart, Qty), Qty > 2,

not Small(Part).
Small(Part) :- Assembly(Part, Subpart, Qty), not Big(Part).
These two rules can be thought of as an attempt to divide parts (those that are mentioned in the
first column of the Assembly table) into two classes, Big and Small. The first rule defines Big to
be the set of parts that use at least three copies of some subpart and that are not classified as small
parts. The second rule defines Small as the set of parts that are not classified as big parts.

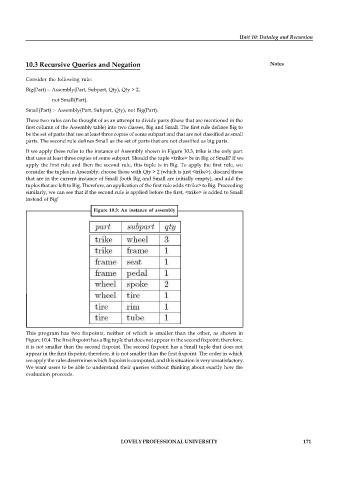
If we apply these rules to the instance of Assembly shown in Figure 10.3, trike is the only part
that uses at least three copies of some subpart. Should the tuple <trike> be in Big or Small? If we
apply the first rule and then the second rule, this tuple is in Big. To apply the first rule, we
consider the tuples in Assembly, choose those with Qty > 2 (which is just <trike>), discard those
that are in the current instance of Small (both Big and Small are initially empty), and add the
tuples that are left to Big. Therefore, an application of the first rule adds <trike> to Big. Proceeding
similarly, we can see that if the second rule is applied before the first, <trike> is added to Small
instead of Big!

Figure 10.3: An instance of assembly

This program has two fixpoints, neither of which is smaller than the other, as shown in
Figure 10.4. The first fixpoint has a Big tuple that does not appear in the second fixpoint; therefore,
it is not smaller than the second fixpoint. The second fixpoint has a Small tuple that does not
appear in the first fixpoint; therefore, it is not smaller than the first fixpoint. The order in which
we apply the rules determines which fixpoint is computed, and this situation is very unsatisfactory.
We want users to be able to understand their queries without thinking about exactly how the
evaluation proceeds.

LOVELY PROFESSIONAL UNIVERSITY 171