Page 4 - DMTH401_REAL ANALYSIS

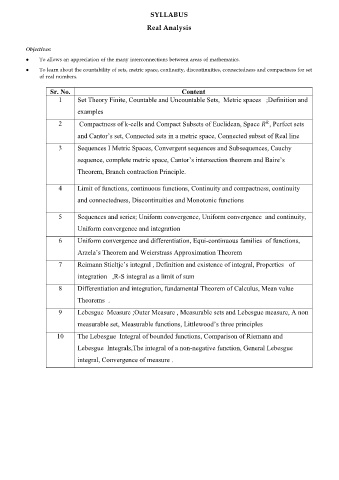
SYLLABUS

Real Analysis

Objectives:

 To allows an appreciation of the many interconnections between areas of mathematics.
 To learn about the countability of sets, metric space, continuity, discontinuities, connectedness and compactness for set
of real numbers.

Sr. No. Content
1 Set Theory Finite, Countable and Uncountable Sets, Metric spaces ;Definition and

examples

2 Compactness of k-cells and Compact Subsets of Euclidean, Space , Perfect sets
and Cantor’s set, Connected sets in a metric space, Connected subset of Real line

3 Sequences I Metric Spaces, Convergent sequences and Subsequences, Cauchy
sequence, complete metric space, Cantor’s intersection theorem and Baire’s

Theorem, Branch contraction Principle.

4 Limit of functions, continuous functions, Continuity and compactness, continuity
and connectedness, Discontinuities and Monotonic functions

5 Sequences and series; Uniform convergence, Uniform convergence and continuity,

Uniform convergence and integration
6 Uniform convergence and differentiation, Equi-continuous families of functions,

Arzela’s Theorem and Weierstrass Approximation Theorem
7 Reimann Stieltje’s integral , Definition and existence of integral, Properties of

integration ,R-S integral as a limit of sum

8 Differentiation and integration, fundamental Theorem of Calculus, Mean value
Theorems .

9 Lebesgue Measure ;Outer Measure , Measurable sets and Lebesgue measure, A non
measurable set, Measurable functions, Littlewood’s three principles

10 The Lebesgue Integral of bounded functions, Comparison of Riemann and

Lebesgue Integrals,The integral of a non-negative function, General Lebesgue
integral, Convergence of measure .