Page 378 - DMTH402_COMPLEX_ANALYSIS_AND_DIFFERENTIAL_GEOMETRY

Unit 30: Geodesic Curvature and Christoffel Symbols

Perhaps surprisingly, there are other surfaces of constant positive curvature besides the sphere. Notes
There are surfaces of constant negative curvature, say K = –1. A famous one is the pseudosphere,
also known as Beltrami’s pseudosphere. This is the surface of revolution obtained by rotating a
curve known as a tractrix around its asymptote. One possible parameterization is given by:
2 cos v
x = ,
e + e –u
u
2 sin v
y = ,
e + e –u
u
e – e –u
u
z = u  ,
e + e –u
u
over ]0, 2[ × .
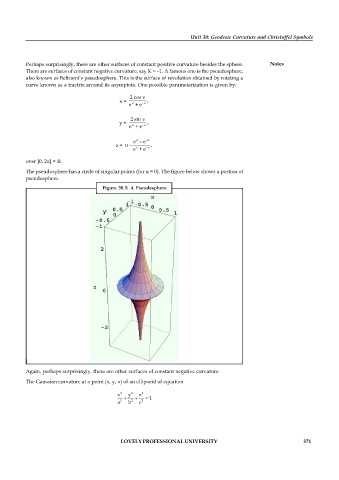
The pseudosphere has a circle of singular points (for u = 0). The figure below shows a portion of
pseudosphere.
Figure 30.3: A Pseudosphere

Again, perhaps surprisingly, there are other surfaces of constant negative curvature.

The Gaussian curvature at a point (x, y, x) of an ellipsoid of equation

x 2 y 2 z 2 1
a 2  b 2  c 2 

LOVELY PROFESSIONAL UNIVERSITY 371