Page 381 - DMTH404_STATISTICS

Unit 27: T - Distributions

Features of t- distribution Notes

2
1. Like c - distribution, t - distribution also has one parameter n = n - 1, where n denotes
sample size. Hence, this distribution is known if n is known.
n
2. Mean of the random variable t is zero and standard deviation is , for n > 2.
n - 2
3. The probability curve of t - distribution is symmetrical about the ordinate at t = 0. Like a
normal variable, the t variable can take any value from -  to .
4. The distribution approaches normal distribution as the number of degrees of freedom
become large.
5. The random variate t is defined as the ratio of a standard normal variate to the square root
c 2
of - variate divided by its degrees of freedom.

X m ( X m- ) n
-
To show this we can write t = =
s/ n s
Dividing numerator and denominator by s, we get

( X m- ) n ( X m- ) ( X m- )
s s / n s / n
t = = =
s 2 2 2
s /s å ( X - X )
s 1 × i
n 1 s 2
-

( X m- )

s / n Standard Normal Variate
= =
2 2
c n 1 c - variate
-
n 1
-
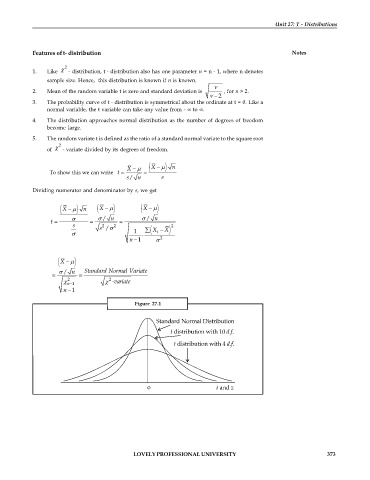
Figure 27.1

LOVELY PROFESSIONAL UNIVERSITY 373