Page 4 - DMTH504_DIFFERENTIAL_AND_INTEGRAL_EQUATION

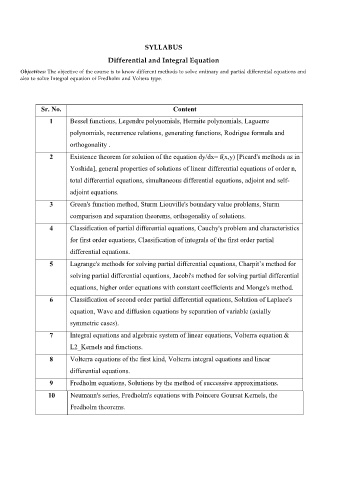
SYLLABUS

Differential and Integral Equation
Objectives: The objective of the course is to know different methods to solve ordinary and partial differential equations and
also to solve Integral equation of Fredholm and Voltera type.

Sr. No. Content

1 Bessel functions, Legendre polynomials, Hermite polynomials, Laguerre

polynomials, recurrence relations, generating functions, Rodrigue formula and
orthogonality .

2 Existence theorem for solution of the equation dy/dx= f(x,y) [Picard's methods as in
Yoshida], general properties of solutions of linear differential equations of order n,

total differential equations, simultaneous differential equations, adjoint and self-

adjoint equations.
3 Green's function method, Sturm Liouville's boundary value problems, Sturm

comparison and separation theorems, orthogonality of solutions.

4 Classification of partial differential equations, Cauchy's problem and characteristics
for first order equations, Classification of integrals of the first order partial

differential equations.
5 Lagrange's methods for solving partial differential equations, Charpit’s method for

solving partial differential equations, Jacobi's method for solving partial differential
equations, higher order equations with constant coefficients and Monge's method.

6 Classification of second order partial differential equations, Solution of Laplace's

equation, Wave and diffusion equations by separation of variable (axially
symmetric cases).

7 Integral equations and algebraic system of linear equations, Volterra equation &

L2_Kernels and functions.
8 Volterra equations of the first kind, Volterra integral equations and linear

differential equations.

9 Fredholm equations, Solutions by the method of successive approximations.
10 Neumann's series, Fredholm's equations with Poincere Goursat Kernels, the

Fredholm theorems.