Page 156 - DMGT209_QUANTITATIVE_TECHNIQUES_II
P. 156
Unit 8: Sampling and Sampling Distribution
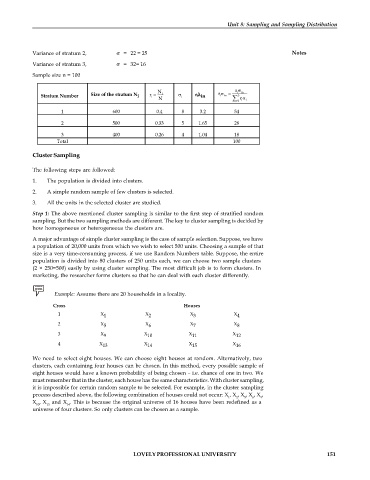
Variance of stratum 2, = 22 = 25 Notes
Variance of stratum 3, = 32= 16
Sample size n = 100
N i r in
i
Stratum Number Size of the stratum N i r i ri in i r 3
in
i
N 1 r i
i
1 600 0.4 8 3.2 54
2 500 0.33 5 1.65 28
3 400 0.26 4 1.04 18
Total 100
Cluster Sampling
The following steps are followed:
1. The population is divided into clusters.
2. A simple random sample of few clusters is selected.
3. All the units in the selected cluster are studied.
Step 1: The above mentioned cluster sampling is similar to the first step of stratified random
sampling. But the two sampling methods are different. The key to cluster sampling is decided by
how homogeneous or heterogeneous the clusters are.
A major advantage of simple cluster sampling is the case of sample selection. Suppose, we have
a population of 20,000 units from which we wish to select 500 units. Choosing a sample of that
size is a very time-consuming process, if we use Random Numbers table. Suppose, the entire
population is divided into 80 clusters of 250 units each, we can choose two sample clusters
(2 × 250=500) easily by using cluster sampling. The most difficult job is to form clusters. In
marketing, the researcher forms clusters so that he can deal with each cluster differently.
Example: Assume there are 20 households in a locality.
Cross Houses
1 X 1 X 2 X 3 X 4
2 X 5 X 6 X 7 X 8
3 X 9 X 10 X 11 X 12
4 X 13 X 14 X 15 X 16
We need to select eight houses. We can choose eight houses at random. Alternatively, two
clusters, each containing four houses can be chosen. In this method, every possible sample of
eight houses would have a known probability of being chosen – i.e. chance of one in two. We
must remember that in the cluster, each house has the same characteristics. With cluster sampling,
it is impossible for certain random sample to be selected. For example, in the cluster sampling
process described above, the following combination of houses could not occur: X , X , X , X , X ,
1 2 5 6 9
X , X and X . This is because the original universe of 16 houses have been redefined as a
10 13 14
universe of four clusters. So only clusters can be chosen as a sample.
LOVELY PROFESSIONAL UNIVERSITY 151