Page 240 - DMGT209_QUANTITATIVE_TECHNIQUES_II
P. 240
Unit 12: Hypothesis Testing
Hoµ = µo, where Ho is the null hypothesis. Alternate hypothesis is HA=µ. The rejection of null Notes
hypothesis will show that the mean of the population is not µ o. This implies that alternate
hypothesis is accepted.
12.2.2 Statistical Significance Level
Having formulated the hypothesis, the next step is its validity at a certain level of significance.
The confidence with which a null hypothesis is accepted or rejected depends upon the significance
level. A significance level of say 5% means that the risk of making a wrong decision is 5%. The
researcher is likely to be wrong in accepting false hypothesis or rejecting a true hypothesis by 5
out of 100 occasions. A significance level of say 1% means, that the researcher is running the risk
of being wrong in accepting or rejecting the hypothesis is one of every 100 occasions. Therefore,
a 1% significance level provides greater confidence to the decision than 5% significance level.
There are two type of tests.
12.2.3 One-tailed and Two-tailed Tests
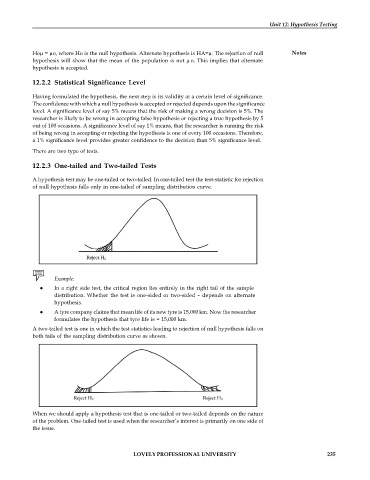
A hypothesis test may be one-tailed or two-tailed. In one-tailed test the test-statistic for rejection
of null hypothesis falls only in one-tailed of sampling distribution curve.
Example:
In a right side test, the critical region lies entirely in the right tail of the sample
distribution. Whether the test is one-sided or two-sided – depends on alternate
hypothesis.
A tyre company claims that mean life of its new tyre is 15,000 km. Now the researcher
formulates the hypothesis that tyre life is = 15,000 km.
A two-tailed test is one in which the test statistics leading to rejection of null hypothesis falls on
both tails of the sampling distribution curve as shown.
When we should apply a hypothesis test that is one-tailed or two-tailed depends on the nature
of the problem. One-tailed test is used when the researcher’s interest is primarily on one side of
the issue.
LOVELY PROFESSIONAL UNIVERSITY 235