Page 115 - DCOM303_DMGT504_OPERATION_RESEARCH

Operations Research

Notes
Example: Solve example 5 by least cost method.
Solution:

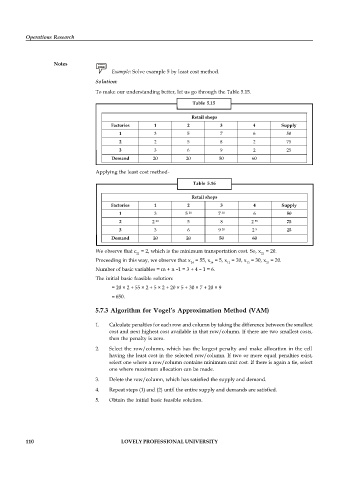
To make our understanding better, let us go through the Table 5.15.
Table 5.15

Retail shops
Factories 1 2 3 4 Supply
1 3 5 7 6 50
2 2 5 8 2 75
3 3 6 9 2 25
Demand 20 20 50 60

Applying the least cost method-

Table 5.16

Retail shops
Factories 1 2 3 4 Supply
1 3 5 7 6 50
30
20
2 2 5 8 2 75
55
20
20
3 3 6 9 2 5 25
Demand 20 20 50 60

We observe that c = 2, which is the minimum transportation cost. So, x = 20.
21 21
Proceeding in this way, we observe that x = 55, x = 5, x = 20, x = 30, x = 20.
24 34 12 13 33
Number of basic variables = m + n –1 = 3 + 4 – 1 = 6.
The initial basic feasible solution:
= 20 × 2 + 55 × 2 + 5 × 2 + 20 × 5 + 30 × 7 + 20 × 9
= 650.

5.7.3 Algorithm for Vogel’s Approximation Method (VAM)

1. Calculate penalties for each row and column by taking the difference between the smallest
cost and next highest cost available in that row/column. If there are two smallest costs,
then the penalty is zero.
2. Select the row/column, which has the largest penalty and make allocation in the cell
having the least cost in the selected row/column. If two or more equal penalties exist,
select one where a row/column contains minimum unit cost. If there is again a tie, select
one where maximum allocation can be made.

3. Delete the row/column, which has satisfied the supply and demand.
4. Repeat steps (1) and (2) until the entire supply and demands are satisfied.
5. Obtain the initial basic feasible solution.

110 LOVELY PROFESSIONAL UNIVERSITY