Page 158 - DCOM504_SECURITY_ANALYSIS_AND_PORTFOLIO_MANAGEMENT

Unit 5: Equity Valuation Models

Solution: Notes
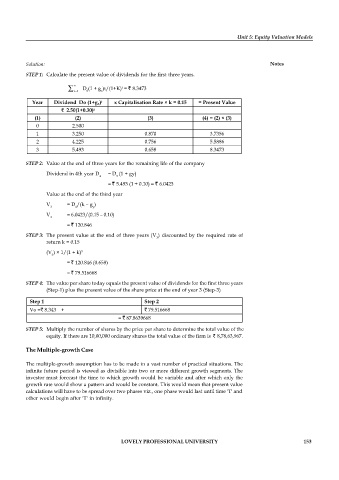
STEP 1: Calculate the present value of dividends for the first three years.
n
D (1 + g )t/(1+K) = 8.3473
t
t=1 0 x
Year Dividend Do (1+g x) t x Capitalisation Rate × k = 0.15 = Present Value
2.50(1+0.30) t
(1) (2) (3) (4) = (2) × (3)
0 2.500
1 3.250 0.870 3.7356
2 4.225 0.756 5.5886
3 5.493 0.658 8.3473

STEP 2: Value at the end of three years for the remaining life of the company

Dividend in 4th year D = D (1 + gy)
4 3
= 5.493 (1 + 0.10) = 6.0423
Value at the end of the third year
V = D /(k – g )
3 4 y
V = 6.0423/(0.15 – 0.10)
3
= 120.846
STEP 3: The present value at the end of three years (V ) discounted by the required rate of
3
return k = 0.15
(V ) × 1/(1 + k) 3
3
= 120.846 (0.658)
= 79.516668

STEP 4: The value per share today equals the present value of dividends for the first three years
(Step-1) plus the present value of the share price at the end of year 3 (Step-3)

Step 1 Step 2
Vo = 8.343 + 79.516668
= 87.8639668

STEP 5: Multiply the number of shares by the price per share to determine the total value of the
equity. If there are 10,00,000 ordinary shares the total value of the firm is 8,78,63,967.

The Multiple-growth Case

The multiple-growth assumption has to be made in a vast number of practical situations. The
infinite future period is viewed as divisible into two or more different growth segments. The
investor must forecast the time to which growth would be variable and after which only the
growth rate would show a pattern and would be constant. This would mean that present value
calculations will have to be spread over two phases viz., one phase would last until time 'T' and
other would begin after 'T' in infinity.

LOVELY PROFESSIONAL UNIVERSITY 153