Page 199 - DCOM505_WORKING_CAPITAL_MANAGEMENT

Working Capital Management

Notes We have
Q
T /T EOQ = [(1/k + k)/2]
= (1/1.2 + 1.2)/2
= 61/60

Thus the cost would increase by 1/60th
Or 240 × 1/60 = ` 4

Graphic Solution

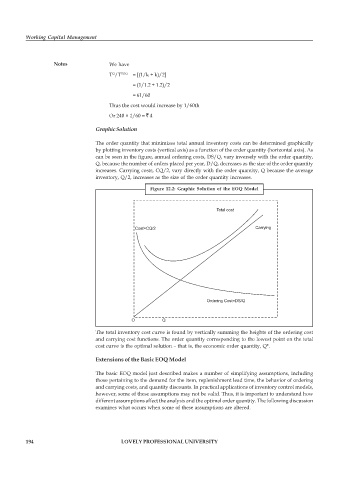
The order quantity that minimizes total annual inventory costs can be determined graphically
by plotting inventory costs (vertical axis) as a function of the order quantity (horizontal axis). As
can be seen in the figure, annual ordering costs, DS/Q, vary inversely with the order quantity,
Q, because the number of orders placed per year, D/Q, decreases as the size of the order quantity
increases. Carrying costs, CQ/2, vary directly with the order quantity, Q because the average
inventory, Q/2, increases as the size of the order quantity increases.

Figure 12.2: Graphic Solution of the EOQ Model

The total inventory cost curve is found by vertically summing the heights of the ordering cost
and carrying cost functions. The order quantity corresponding to the lowest point on the total
cost curve is the optimal solution – that is, the economic order quantity, Q*.

Extensions of the Basic EOQ Model

The basic EOQ model just described makes a number of simplifying assumptions, including
those pertaining to the demand for the item, replenishment lead time, the behavior of ordering
and carrying costs, and quantity discounts. In practical applications of inventory control models,
however, some of these assumptions may not be valid. Thus, it is important to understand how
different assumptions affect the analysis and the optimal order quantity. The following discussion
examines what occurs when some of these assumptions are altered.

194 LOVELY PROFESSIONAL UNIVERSITY