Page 12 - DCAP108_DIGITAL_CIRCUITS_AND_LOGIC_DESIGNS

Unit 1: Number Systems

the octal number system up to 3 decimal places before and 2 decimal places after the octal point (.). Notes
Table 1.2: Octal Weights

Weights 8 2 8 1 8 0 . 8 –1 8 –2
Just like the other counting conventions discussed previously, the LSB begins with zero (0) and is
incremented until the maximum digit value is reached. The adjacent bit positions are then filled
appropriately as the iterative counting process continues. Thus the counting convention for octal
is 0, 1, 2, 3, 4, 5, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20 ..........
The octal, or base 8, number system is a common system used with computers. Because of its
relationship with the binary system, it is useful in programming some types of computers.
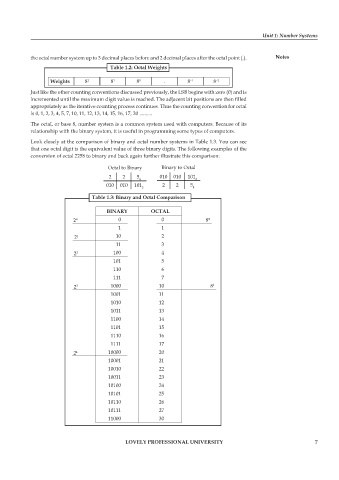
Look closely at the comparison of binary and octal number systems in Table 1.3. You can see
that one octal digit is the equivalent value of three binary digits. The following examples of the
conversion of octal 2258 to binary and back again further illustrate this comparison:

Octal to Binary Binary to Octal
2 2 5 010 010 101
8 2
010 010 101 2 2 2 5 8
Table 1.3: Binary and Octal Comparison

BINARY OCTAL
2° 0 0 8°
1 1
2 1 10 2
11 3
2 2 100 4
101 5
110 6
111 7
2 3 1000 10 8 1
1001 11
1010 12
1011 13
1100 14
1101 15
1110 16
1111 17
2 4 10000 20
10001 21
10010 22
10011 23
10100 24
10101 25
10110 26
10111 27
11000 30

LOVELY PROFESSIONAL UNIVERSITY 7