Page 224 - DMTH201_Basic Mathematics-1
P. 224
Unit 7: Limits
On combining the results of these two limits, we can say that demand increases from zero to Notes
infinitely large amount as the price falls.
We can write total revenue as
Further,
which implies that total revenue increases to a limiting value a.
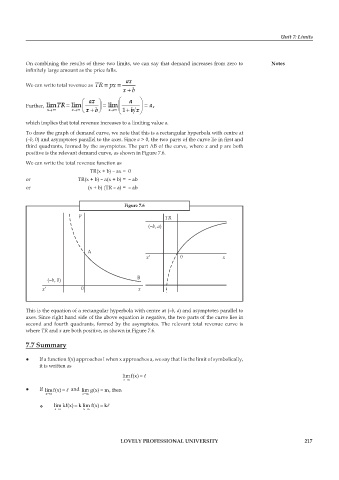
To draw the graph of demand curve, we note that this is a rectangular hyperbola with centre at
(–b, 0) and asymptotes parallel to the axes. Since a > 0, the two parts of the curve lie in first and
third quadrants, formed by the asymptotes. The part AB of the curve, where x and p are both
positive is the relevant demand curve, as shown in Figure 7.6.
We can write the total revenue function as
TR(x + b) – ax = 0
or TR(x + b) – a(x + b) = – ab
or (x + b) (TR – a) = – ab
Figure 7.6
p TR
a
(– , )
b
A
x′ 0 x
B
(– , 0)
b
x′ 0 x
This is the equation of a rectangular hyperbola with centre at (–b, a) and asymptotes parallel to
axes. Since right hand side of the above equation is negative, the two parts of the curve lies in
second and fourth quadrants, formed by the asymptotes. The relevant total revenue curve is
where TR and x are both positive, as shown in Figure 7.6.
7.7 Summary
z z If a function f(x) approaches l when x approaches a, we say that l is the limit of symbolically,
it is written as
lim ( ) = l
f
x
xÆ a
z z If lim ( )f x = l and lim ( )g x = m , then
xÆ a xÆ a
=
=
x
x
f
lim kf ( ) k lim ( ) kl
x Æ a x Æ a
LOVELY PROFESSIONAL UNIVERSITY 217