Page 54 - DMGT409Basic Financial Management

Unit 3: Time Value of Money

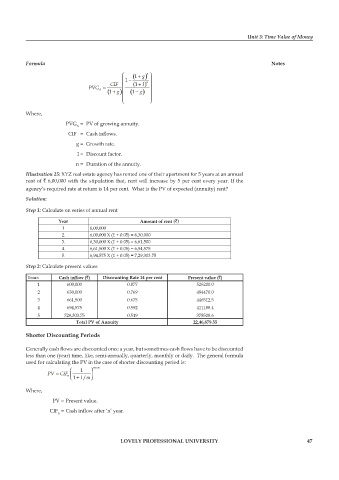
Formula Notes

)
⎛ ( 1 g ⎞
n
+
⎜ 1 − n ⎟
+
CIF ⎜ (1 I ) ⎟
PVG = (1 g ⎜ ( 1 g ) ⎟
)
A
−
+
⎜ ⎜ ⎝ ⎟ ⎟ ⎠
Where,
PVG = PV of growing annuity.
A
CIF = Cash infl ows.
g = Growth rate.
I = Discount factor.
n = Duration of the annuity.

Illustration 25: XYZ real estate agency has rented one of their apartment for 5 years at an annual
rent of ` 6,00,000 with the stipulation that, rent will increase by 5 per cent every year. If the
agency’s required rate at return is 14 per cent. What is the PV of expected (annuity) rent?
Solution:
Step 1: Calculate on series of annual rent

Year Amount of rent (`)
1 6,00,000
2. 6,00,000 X (1 + 0.05) = 6,30,000
3. 6,30,000 X (1 + 0.05) = 6,61,500
4. 6,61,500 X (1 + 0.05) = 6,94,575
5. 6,94,575 X (1 + 0.05) = 7,29,303.75

Step 2: Calculate present values
Years Cash infl ow (`) Discounting Rate 14 per cent Present value (`)
1 600,000 0.877 526200.0
2 630,000 0.769 484470.0
3 661,500 0.675 446512.5
4 694,575 0.592 411188.4
5 729,303.75 0.519 378508.6
Total PV of Annuity 22,46,879.55

Shorter Discounting Periods

Generally cash flows are discounted once a year, but sometimes cash flows have to be discounted

less than one (year) time, like, semi-annually, quarterly, monthly or daily. The general formula
used for calculating the PV in the case of shorter discounting period is:
×
⎛ 1 ⎞ mn
PV = CIF n ⎜ ⎟
1 Im⎠
⎝ + /
Where,
PV = Present value.
CIF = Cash infl ow after ‘n’ year.
n

LOVELY PROFESSIONAL UNIVERSITY 47