Page 34 - DCAP407_DATA_STRUCTURE
P. 34
Unit 2: Complexity Analysis
Consider a sequence x1, x2, x3……x10. The simple addition of this sequence is
x1+x2+x3+x4+x5+x6+x7+x8+x9+x10. Using mathematical notation we can
shorten the addition. It can be done by using a symbol to denote “all the way up
to” or “all the way down to”.
Then, the expression will be x1+x2+x3+…..+x10. We can also represent the
expression using Greek letter Σ as shown below:
b
∑ var iable index var iable
index var iable =a
Here, a is the first index and b is the last index. The variables are the numbers
that appear constantly in all terms. In the expression,
x1+x2+x3+x4+x5+x6+x7+x8+x9+x10
1 is the first index, 10 is the last index, and x is the variable. If we use i as the
index variable then the expression will be
10
∑ x i
i =1
Exponent and Logarithm
Exponential function has the form f(x) =a +B where, a is the base, x is the exponent, and B is any
x
expression.
If a is positive, the function continuously increases in value. As x increases, the slope of the function also
increases.
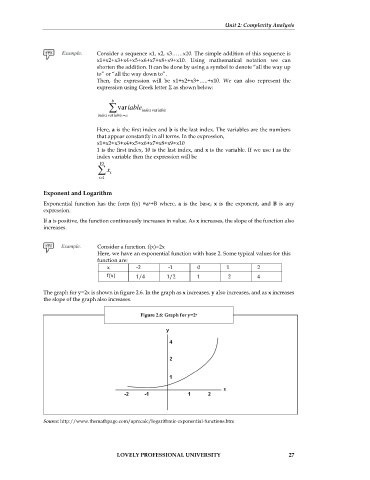
Consider a function. f(x)=2x
Here, we have an exponential function with base 2. Some typical values for this
function are:
x -2 -1 0 1 2
) x ( f 1/4 1/2 1 2 4
The graph for y=2x is shown in figure 2.6. In the graph as x increases, y also increases, and as x increases
the slope of the graph also increases.
Figure 2.6: Graph for y=2 x
Source: http://www.themathpage.com/aprecalc/logarithmic-exponential-functions.htm
LOVELY PROFESSIONAL UNIVERSITY 27