Page 87 - DCAP504_Computer Graphics

Computer Graphics

with the product matrix of scaling and rotation matrices.
The product of scaling matrix and rotation matrix:
.
 50. 0  0 0 −1  0   0 − 5  0 
0


 
T =  0 0. 5  0 1 0  0 =  50. 0  0
     
 0 0 1   0 0 1   0 0 1 
where, T is the product of scaling matrix and rotation matrix.
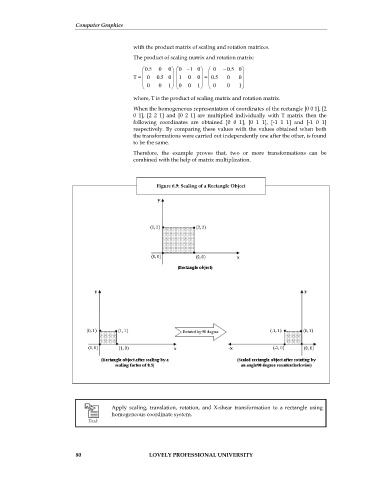
When the homogeneous representation of coordinates of the rectangle [0 0 1], [2
0 1], [2 2 1] and [0 2 1] are multiplied individually with T matrix then the
following coordinates are obtained [0 0 1], [0 1 1], [-1 1 1] and [-1 0 1]
respectively. By comparing these values with the values obtained when both
the transformations were carried out independently one after the other, is found
to be the same.
Therefore, the example proves that, two or more transformations can be
combined with the help of matrix multiplication.

Figure 6.9: Scaling of a Rectangle Object

Apply scaling, translation, rotation, and X-shear transformation to a rectangle using
homogeneous coordinate system.

80 LOVELY PROFESSIONAL UNIVERSITY