Page 274 - DCAP605_ADVANCED_DATA_STRUCTURE_AND_ALGORITHMS

Unit 13: Graphs

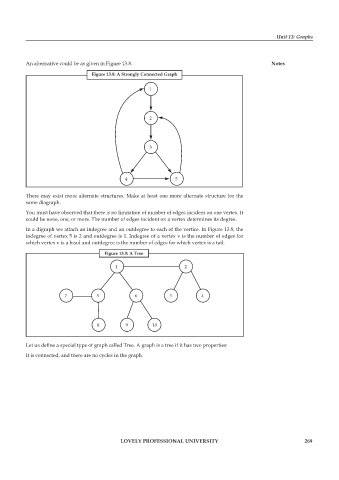
An alternative could be as given in Figure 13.8. Notes

Figure 13.8: A Strongly Connected Graph

1

2

3

4 5

There may exist more alternate structures. Make at least one more alternate structure for the
same diagraph.
You must have observed that there is no limitation of number of edges incident on one vertex. It
could be none, one, or more. The number of edges incident on a vertex determines its degree.

In a digraph we attach an indegree and an outdegree to each of the vertice. In Figure 13.8, the
indegree of vertex 5 is 2 and outdegree is 1. Indegree of a vertex v is the number of edges for
which vertex v is a head and outdegree is the number of edges for which vertex is a tail.

Figure 13.9: A Tree

1 2

7 5 6 3 4

8 9 10

Let us define a special type of graph called Tree. A graph is a tree if it has two properties:

It is connected, and there are no cycles in the graph.

LOVELY PROFESSIONAL UNIVERSITY 269