Page 40 - DMGT409Basic Financial Management

Unit 3: Time Value of Money

Formula: Notes

×
⎡ i ⎤ mn
A = P ⎢ ⎣ 1 + m⎦ ⎥
Where,
A = Amount after a period.
P = Amount in the beginning of the period.
I = Interest rate.
M = Number of times per year compounding is made.

n = Number of years for which compounding is to be done.

3.3.2 Future Value of Series of Cash Flows

So far we have considered only the future value of a single payment made at time zero. The
transactions in real life are not limited to one. An investor investing money in installments may
wish to know the value of his savings after ‘n’ years.
Illustration 2: Mr. Manoj invests ` 500, ` 1,000, ` 1,500, ` 2,000 and ` 2,500 at the end of each year.
Calculate the compound value at the end of 5 years, compounded annually, when the interest
charged is 5% p.a.
Solution:
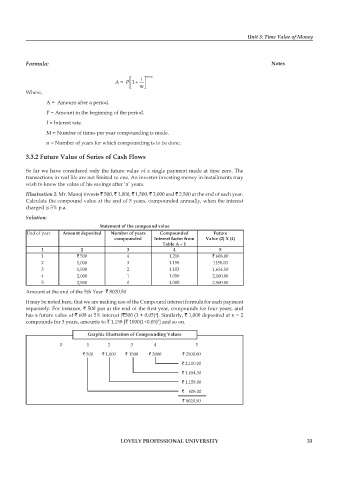
Statement of the compound value
End of year Amount deposited Number of years Compounded Future
compounded Interest factor from Value (2) X (4)
Table A – 1
1 2 3 4 5
1 ` 500 4 1.216 ` 608.00
2 1,000 3 1.158 1158.00
3 1,500 2 1.103 1,654.50
4 2,000 1 1.050 2,100.00
5 2,500 0 1.000 2,500.00
Amount at the end of the 5th Year ` 8020.50

It may be noted here, that we are making use of the Compound interest formula for each payment
separately. For instance, ` 500 put at the end of the first year, compounds for four years, and

has a future value of ` 608 at 5% interest [`500 (1 + 0.05) ]. Similarly, ` 1,000 deposited at n = 2
4
3
compounds for 3 years, amounts to ` 1,158 [` 1000(1+0.05) ] and so on.
Graphic illustration of Compounding Values
0 1 2 3 4 5
` 500 ` 1,000 ` 1500 ` 2000 ` 2500.00
` 2,100.00
` 1,654.50
` 1,158.00
` 608.00
` 8020.50

LOVELY PROFESSIONAL UNIVERSITY 33