Page 146 - DCAP504_Computer Graphics

Unit 9: Clipping I

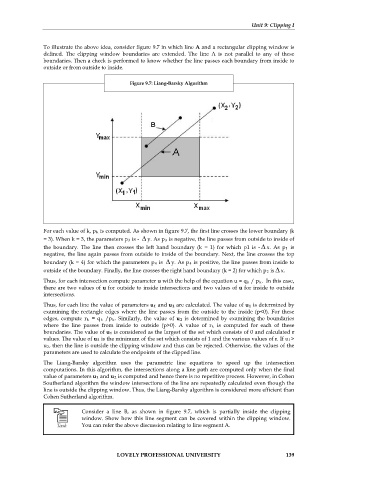
To illustrate the above idea, consider figure 9.7 in which line A and a rectangular clipping window is
defined. The clipping window boundaries are extended. The line A is not parallel to any of these
boundaries. Then a check is performed to know whether the line passes each boundary from inside to
outside or from outside to inside.

Figure 9.7: Liang-Barsky Algorithm

For each value of k, p k is computed. As shown in figure 9.7, the first line crosses the lower boundary (k
= 3). When k = 3, the parameters p 3 is - ∆ y. As p 3 is negative, the line passes from outside to inside of
the boundary. The line then crosses the left hand boundary (k = 1) for which p1 is - ∆ x. As p 1 is
negative, the line again passes from outside to inside of the boundary. Next, the line crosses the top
boundary (k = 4) for which the parameters p 4 is ∆ y. As p 4 is positive, the line passes from inside to
is
outside of the boundary. Finally, the line crosses the right hand boundary (k = 2) for which p 2 ∆ x.
Thus, for each intersection compute parameter u with the help of the equation u = q k / p k. In this case,
there are two values of u for outside to inside intersections and two values of u for inside to outside
intersections.
Thus, for each line the value of parameters u 1 and u 2 are calculated. The value of u 1 is determined by
examining the rectangle edges where the line passes from the outside to the inside (p<0). For these
edges, compute r k = q k /p k. Similarly, the value of u 2 is determined by examining the boundaries
where the line passes from inside to outside (p>0). A value of r k is computed for each of these
boundaries. The value of u 1 is considered as the largest of the set which consists of 0 and calculated r
values. The value of u 2 is the minimum of the set which consists of 1 and the various values of r. If u 1>
u 2, then the line is outside the clipping window and thus can be rejected. Otherwise, the values of the
parameters are used to calculate the endpoints of the clipped line.
The Liang-Barsky algorithm uses the parametric line equations to speed up the intersection
computations. In this algorithm, the intersections along a line path are computed only when the final
value of parameters u 1 and u 2 is computed and hence there is no repetitive process. However, in Cohen
Southerland algorithm the window intersections of the line are repeatedly calculated even though the
line is outside the clipping window. Thus, the Liang-Barsky algorithm is considered more efficient than
Cohen Sutherland algorithm.

Consider a line B, as shown in figure 9.7, which is partially inside the clipping
window. Show how this line segment can be covered within the clipping window.
You can refer the above discussion relating to line segment A.

LOVELY PROFESSIONAL UNIVERSITY 139