Page 71 - DCAP504_Computer Graphics

Computer Graphics

6.1 Transformation Matrix

2-D graphic objects can be represented using a set of points on a simple graph of X and Y axis. The
coordinate values of the points that make the object are used to determine the position and size of the
object. A 2-D transformation is nothing but mapping or transforming a 2-D point. When 2-D
transformation is applied to a 2-D point, it is transformed to another 2-D point in the 2-D space. This
means that a 2-D point P=(x, y) transforms to P'=(x', y') after transformation.

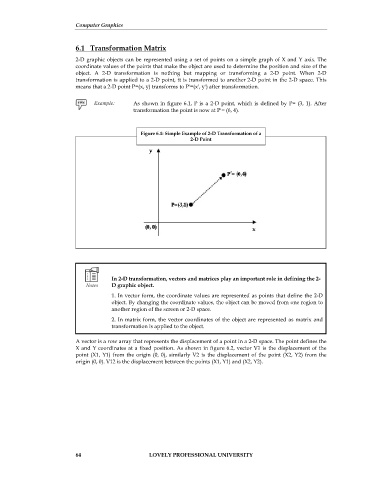
As shown in figure 6.1, P is a 2-D point, which is defined by P= (3, 1). After
transformation the point is now at P'= (6, 4).

Figure 6.1: Simple Example of 2-D Transformation of a
2-D Point

In 2-D transformation, vectors and matrices play an important role in defining the 2-
D graphic object.
1. In vector form, the coordinate values are represented as points that define the 2-D
object. By changing the coordinate values, the object can be moved from one region to
another region of the screen or 2-D space.
2. In matrix form, the vector coordinates of the object are represented as matrix and
transformation is applied to the object.

A vector is a row array that represents the displacement of a point in a 2-D space. The point defines the
X and Y coordinates at a fixed position. As shown in figure 6.2, vector V1 is the displacement of the
point (X1, Y1) from the origin (0, 0), similarly V2 is the displacement of the point (X2, Y2) from the
origin (0, 0). V12 is the displacement between the points (X1, Y1) and (X2, Y2).

64 LOVELY PROFESSIONAL UNIVERSITY