Page 208 - DMTH201_Basic Mathematics-1

Unit 7: Limits

Notes

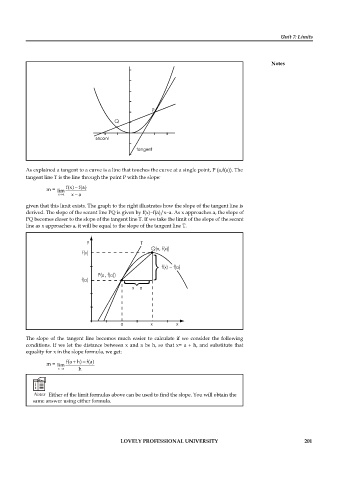
As explained a tangent to a curve is a line that touches the curve at a single point, P (a,f(a)). The
tangent line T is the line through the point P with the slope:

m =

given that this limit exists. The graph to the right illustrates how the slope of the tangent line is
derived. The slope of the secant line PQ is given by f(x)–f(a)/x–a. As x approaches a, the slope of
PQ becomes closer to the slope of the tangent line T. If we take the limit of the slope of the secant
line as x approaches a, it will be equal to the slope of the tangent line T.

The slope of the tangent line becomes much easier to calculate if we consider the following
conditions. If we let the distance between x and a be h, so that x= a h, and substitute that
equality for x in the slope formula, we get:
m =

Either of the limit formulas above can be used to find the slope. You will obtain the
same answer using either formula.

LOVELY PROFESSIONAL UNIVERSITY 201