Page 101 - DECO101_MICRO_ECONOMICS_ENGLISH

Micro Economics

Notes
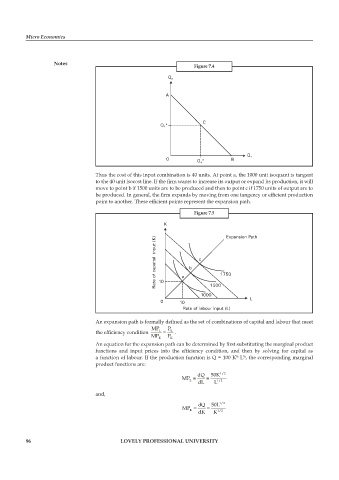
Figure 7.4

Thus the cost of this input combination is 40 units. At point a, the 1000 unit isoquant is tangent

to the 40 unit isocost line. If the firm wants to increase its output or expand its production, it will
move to point b if 1500 units are to be produced and then to point c if 1750 units of output are to

be produced. In general, the firm expands by moving from one tangency or effi cient production

point to another. These efficient points represent the expansion path.
Figure 7.5

An expansion path is formally defined as the set of combinations of capital and labour that meet

MP P
the effi ciency condition L = L .
MP K P K

An equation for the expansion path can be determined by first substituting the marginal product
functions and input prices into the efficiency condition, and then by solving for capital as

½
½
a function of labour. If the production function is Q = 100 K L , the corresponding marginal
product functions are:
dQ 50K 1/2
MP = = 1/2
L
dL L
and,
dQ 50L 1/2
MP = =
K
dK K 1/2

96 LOVELY PROFESSIONAL UNIVERSITY