Page 108 - DECO101_MICRO_ECONOMICS_ENGLISH

Unit 8: Laws of Production

amount of labour, it experiences the law of variable proportion or diminishing marginal returns. Notes
This law states that,
As more and more of the factor input is employed, all other input quantities remaining constant,

a point will finally be reached where additional quantities of varying input will produce
diminishing marginal contributions to total product.
This underlines the short run production function. It can be shown in a Table 8.1 and Figure 8.1
as follows.
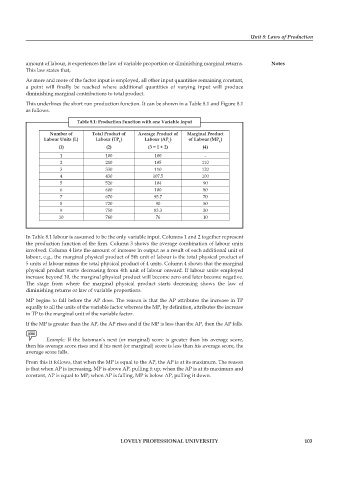
Table 8.1: Production Function with one Variable Input

Number of Total Product of Average Product of Marginal Product
Labour Units (L) Labour (TP ) Labour (AP ) of Labour (MP )
L
L
L
(1) (2) (3 = 1 + 2) (4)
1 100 100 –
2 210 105 110
3 330 110 120
4 430 107.5 100
5 520 104 90
6 600 100 80
7 670 95.7 70
8 720 90 50
9 750 83.3 30
10 760 76 10

In Table 8.1 labour is assumed to be the only variable input. Columns 1 and 2 together represent
the production function of the firm. Column 3 shows the average combination of labour units

involved. Column 4 lists the amount of increase in output as a result of each additional unit of
labour, e.g., the marginal physical product of 5th unit of labour is the total physical product of
5 units of labour minus the total physical product of 4 units. Column 4 shows that the marginal
physical product starts decreasing from 4th unit of labour onward. If labour units employed
increase beyond 10, the marginal physical product will become zero and later become negative.
The stage from where the marginal physical product starts decreasing shows the law of
diminishing returns or law of variable proportions.
MP begins to fall before the AP does. The reason is that the AP attributes the increase in TP
equally to all the units of the variable factor whereas the MP, by definition, attributes the increase

in TP to the marginal unit of the variable factor.
If the MP is greater than the AP, the AP rises and if the MP is less than the AP, then the AP falls.

Example: If the batsman’s next (or marginal) score is greater than his average score,
then his average score rises and if his next (or marginal) score is less than his average score, the
average score falls.

From this it follows, that when the MP is equal to the AP, the AP is at its maximum. The reason
is that when AP is increasing, MP is above AP, pulling it up; when the AP is at its maximum and
constant, AP is equal to MP; when AP is falling, MP is below AP, pulling it down.

LOVELY PROFESSIONAL UNIVERSITY 103