Page 309 - DCOM203_DMGT204_QUANTITATIVE_TECHNIQUES_I
P. 309
Quantitative Techniques – I
Notes
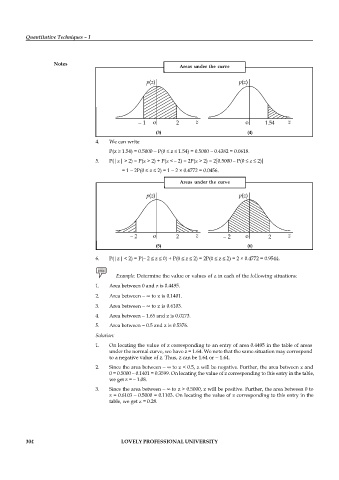
Areas under the curve
(3) (4)
4. We can write
P(z 1.54) = 0.5000 P(0 z 1.54) = 0.5000 0.4382 = 0.0618.
5. P(|z| > 2) = P(z > 2) + P(z < 2) = 2P(z > 2) = 2[0.5000 P(0 z 2)]
= 1 2P(0 z 2) = 1 2 × 0.4772 = 0.0456.
Areas under the curve
(5) (6)
6. P(|z| < 2) = P( 2 z 0) + P( z 2) = 2P( z 2) = 2 × 0.4772 = 0.9544.
Example: Determine the value or values of z in each of the following situations:
1. Area between 0 and z is 0.4495.
2. Area between to z is 0.1401.
3. Area between to z is 0.6103.
4. Area between 1.65 and z is 0.0173.
5. Area between 0.5 and z is 0.5376.
Solution:
1. On locating the value of z corresponding to an entry of area 0.4495 in the table of areas
under the normal curve, we have z = 1.64. We note that the same situation may correspond
to a negative value of z. Thus, z can be 1.64 or 1.64.
2. Since the area between to z < 0.5, z will be negative. Further, the area between z and
0 = 0.5000 0.1401 = 0.3599. On locating the value of z corresponding to this entry in the table,
we get z = 1.08.
3. Since the area between to z > 0.5000, z will be positive. Further, the area between 0 to
z = 0.6103 0.5000 = 0.1103. On locating the value of z corresponding to this entry in the
table, we get z = 0.28.
304 LOVELY PROFESSIONAL UNIVERSITY