Page 39 - DCOM203_DMGT204_QUANTITATIVE_TECHNIQUES_I
P. 39
Quantitative Techniques – I
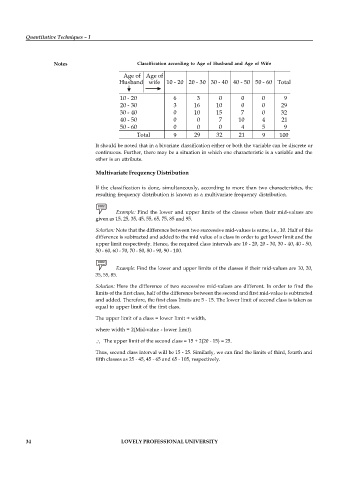
Notes Classification according to Age of Husband and Age of Wife
Age of Age of
Husband wife 10 - 20 20 - 30 30 - 40 40 - 50 50 - 60 Total
10 - 20 6 3 0 0 0 9
20 - 30 3 16 10 0 0 29
30 - 40 0 10 15 7 0 32
40 - 50 0 0 7 10 4 21
50 - 60 0 0 0 4 5 9
Total 9 29 32 21 9 100
It should be noted that in a bivariate classification either or both the variable can be discrete or
continuous. Further, there may be a situation in which one characteristic is a variable and the
other is an attribute.
Multivariate Frequency Distribution
If the classification is done, simultaneously, according to more than two characteristics, the
resulting frequency distribution is known as a multivariate frequency distribution.
Example: Find the lower and upper limits of the classes when their mid-values are
given as 15, 25, 35, 45, 55, 65, 75, 85 and 95.
Solution: Note that the difference between two successive mid-values is same, i.e., 10. Half of this
difference is subtracted and added to the mid value of a class in order to get lower limit and the
upper limit respectively. Hence, the required class intervals are 10 - 20, 20 - 30, 30 - 40, 40 - 50,
50 - 60, 60 - 70, 70 - 80, 80 - 90, 90 - 100.
Example: Find the lower and upper limits of the classes if their mid-values are 10, 20,
35, 55, 85.
Solution: Here the difference of two successive mid-values are different. In order to find the
limits of the first class, half of the difference between the second and first mid-value is subtracted
and added. Therefore, the first class limits are 5 - 15. The lower limit of second class is taken as
equal to upper limit of the first class.
The upper limit of a class = lower limit + width,
where width = 2(Mid-value - lower limit).
The upper limit of the second class = 15 + 2(20 - 15) = 25.
Thus, second class interval will be 15 - 25. Similarly, we can find the limits of third, fourth and
fifth classes as 25 - 45, 45 - 65 and 65 - 105, respectively.
34 LOVELY PROFESSIONAL UNIVERSITY