Page 104 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 5: Transportation Problem

5.1.3 General Representation of Transportation Model Notes

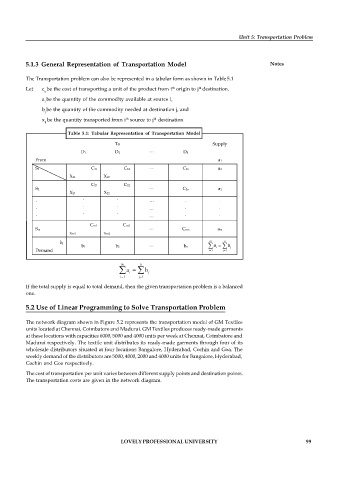
The Transportation problem can also be represented in a tabular form as shown in Table 5.1
th
th
Let c be the cost of transporting a unit of the product from i origin to j destination.
ij
a be the quantity of the commodity available at source i,
i
b be the quantity of the commodity needed at destination j, and
j
x be the quantity transported from i source to j destination
th
th
ij
Table 5.1: Tabular Representation of Transportation Model
To Supply
D1 D2  D3
From a1
S1 C11 C12  C1n a1
X11 X12
C21 C22
S2  C2n a2
X21 X22
. .
.  . .
. .
.  . .
. .
. . .

Cm1 Cm2
Sm  Cmn am
xm1 xm2
bj m n
b1 b2  bn  a i   b
j
Demand  i 1  j 1

  
 
If the total supply is equal to total demand, then the given transportation problem is a balanced
one.

5.2 Use of Linear Programming to Solve Transportation Problem

The network diagram shown in Figure 5.2 represents the transportation model of GM Textiles
units located at Chennai, Coimbatore and Madurai. GM Textiles produces ready-made garments
at these locations with capacities 6000, 5000 and 4000 units per week at Chennai, Coimbatore and
Madurai respectively. The textile unit distributes its ready-made garments through four of its
wholesale distributors situated at four locations Bangalore, Hyderabad, Cochin and Goa. The
weekly demand of the distributors are 5000, 4000, 2000 and 4000 units for Bangalore, Hyderabad,
Cochin and Goa respectively.
The cost of transportation per unit varies between different supply points and destination points.
The transportation costs are given in the network diagram.

LOVELY PROFESSIONAL UNIVERSITY 99