Page 72 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 3: Linear Programming Problem – Simplex Method

Step 3: Bring the objective function into a standard form. Notes
Maximise ‘Z’ = – 12x – 20x – x + x – Mx – Mx
1 2 3 4 5 6
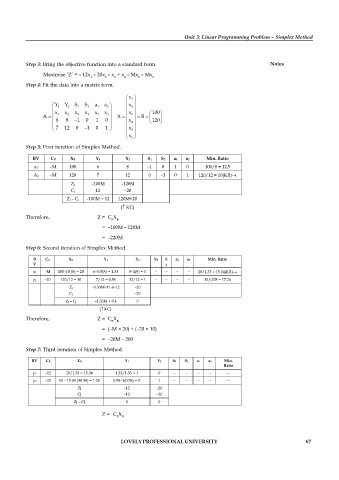
Step 4: Fit the data into a matrix form.

 x 1 
 
 Y 1 Y 2 S 1 S 2 a 1 a 2   x 2 
 x x x x x x   x   100
A   1 2 3 4 5 6  X   3   B    
 6 8 1 0 1 0   x   120 
     4 
 7 12 0 1 0 1  x 5
 
 x 
 6 
Step 5: First iteration of Simplex Method.
BV CB XB Y1 Y2 S1 S2 a1 a2 Min. Ratio
a1 –M 100 6 8 –1 0 1 0 100/8 = 12.5
A2 –M 120 7 12 0 –1 0 1 120/12 = 10(KR)
Zj –100M –120M
Cj 12 –20
Zj – Cj –100M + 12 120M+20
( KC)
Therefore, Z = C X
B B
= –100M – 120M

= –220M
Step 6: Second iteration of Simplex Method.
B CB XB Y1 Y2 S1 S a1 a2 Min. Ratio
V 2
a1 –M 100–10 (8) = 20 6–0.5(8) = 1.33 8–1(8) = 0 – – – – 20/1.33 = 15.04(KR)
y2 –20 120/12 = 10 7/12 = 0.58 12/12 = 1 – – – – 10/0.58 = 17.24
Zj –1.33M–11.6–12 –20
Cj –20
Zj – Cj –1.33M + 0.4 0
( KC)
Therefore, Z = C X
B B
= (–M × 20) + (–20 × 10)
= –20M – 200
Step 7: Third iteration of Simplex Method.

BV CB XB Y1 Y2 S1 S2 a1 a2 Min.
Ratio
y1 –12 20/1.33 = 15.04 1.33/1.33 = 1 0 – – – – ––
y2 –20 10 – 15.04 (90.58) = 1.28 0.58–1(0.58) = 0 1 – – – – ––
Zj –12 –20
Cj –12 –20
Zj – Cj 0 0

Z = C X
B B

LOVELY PROFESSIONAL UNIVERSITY 67