Page 149 - DECO401_MICROECONOMIC_THEORY_ENGLISH

Microeconomic Theory

Notes By substituting this function into observed function a function is obtained which expresses the minimum
level of expenditure which can earn utility level U, on given costs P,

∑ P f (P, U) …(3)
i i i
This is customer’s expenditure function.
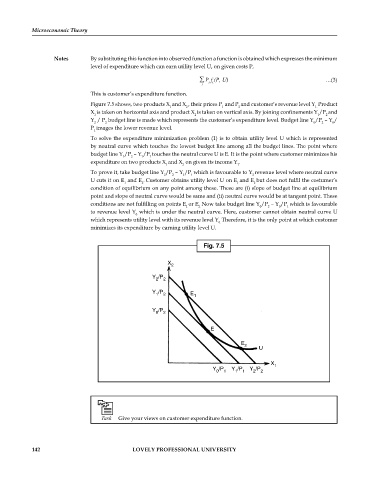
Figure 7.5 shows, two products X and X , their prices P and P and customer’s revenue level Y Product
2
1.
1
1
2
X is taken on horizontal axis and product X is taken on vertical axis. By joining confinements Y /P and
1
1
2
2
Y / P budget line is made which represents the customer’s expenditure level. Budget line Y /P – Y /
2
0
2
2
0
P images the lower revenue level.
1
To solve the expenditure minimization problem (1) is to obtain utility level U which is represented
by neutral curve which touches the lowest budget line among all the budget lines. The point where
budget line Y /P – Y /P touches the neutral curve U is E. It is the point where customer minimizes his
1 2 1 1
expenditure on two products X and X on given its income Y .
1 2 1
To prove it, take budget line Y /P – Y /P which is favourable to Y revenue level where neutral curve
2 2 1 1 2
U cuts it on E and E . Customer obtains utility level U on E and E but does not fulfil the costumer’s
1 2 1 2
condition of equilibrium on any point among these. These are (i) slope of budget line at equilibrium
point and slope of neutral curve would be same and (ii) neutral curve would be at tangent point. These
conditions are not fulfilling on points E or E Now take budget line Y /P – Y /P which is favourable
1 2. 0 2 0 1
to revenue level Y which is under the neutral curve. Here, customer cannot obtain neutral curve U
0
which represents utility level with its revenue level Y Therefore, it is the only point at which customer
0.
minimizes its expenditure by earning utility level U.
Fig. 7.5
X
2
Y /P
2 2
Y /P
1 2 E 1
Y /P
0 2
E
E
2
U
X 1
Y /P Y /P Y /P
0 1 1 1 2 2

Give your views on customer expenditure function.

142 LOVELY PROFESSIONAL UNIVERSITY