Page 304 - DECO504_STATISTICAL_METHODS_IN_ECONOMICS_ENGLISH

Unit 23 : Time Series Methods—Graphic, Method of Semi-averages

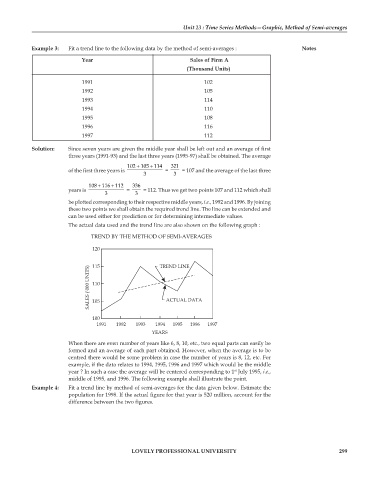
Example 3: Fit a trend line to the following data by the method of semi-averages : Notes

Year Sales of Firm A
(Thousand Units)
1991 102
1992 105
1993 114
1994 110
1995 108
1996 116
1997 112

Solution: Since seven years are given the middle year shall be left out and an average of first
three years (1991-93) and the last three years (1995-97) shall be obtained. The average
+
+
102 105 114 321
of the first three years is = = 107 and the average of the last three
3 3
+
+
108 116 112 336
years is = = 112. Thus we get two points 107 and 112 which shall
3 3
be plotted corresponding to their respective middle years, i.e., 1992 and 1996. By joining
these two points we shall obtain the required trend line. The line can be extended and
can be used either for prediction or for determining intermediate values.
The actual data used and the trend line are also shown on the following graph :
TREND BY THE METHOD OF SEMI-AVERAGES

120 TREND LINE

115
SALES (’000 UNITS) 110 ACTUAL DATA

105

100
1991 1992 1993 1994 1995 1996 1997
YEARS
When there are even number of years like 6, 8, 10, etc., two equal parts can easily be
formed and an average of each part obtained. However, when the average is to be
centred there would be some problem in case the number of years is 8, 12, etc. For
example, if the data relates to 1994, 1995, 1996 and 1997 which would be the middle
year ? In such a case the average will be centered corresponding to 1 July 1995, i.e.,
st
middle of 1995, and 1996. The following example shall illustrate the point.
Example 4: Fit a trend line by method of semi-averages for the data given below. Estimate the
population for 1998. If the actual figure for that year is 520 million, account for the
difference between the two figures.

LOVELY PROFESSIONAL UNIVERSITY 299