Page 176 - DEDU504_EDUCATIONAL_MEASUREMENT_AND_EVALUATION_ENGLISH

Educational Measurement and Evaluation

Notes 13.1.1 Percentile Rank
An individual’s percentile rank on a test designates the percentage of cases or scores lying below
it. Thus a person having a percentile rank of 20 (P ) is situated above twenty percent of the group
20
of which he is member; or, otherwise stated, twenty percent of the group fall below this person’s
rank. A percentile rank of 70 (P ) means that seventy percent fall below—and so on, for any
70
percentile rank in the scale. In effect, this statistical device makes it possible to determine at
which one-hundredth part of the distribution of scores or cases any particular individual is
located. By this means a person’s relative status, or position in the group, can be established with
respect to the traits or functions being tested. And, as will be seen, psychological measurement,
unlike physical measurement, derives its significance principally from relative ranks ascribed to
individuals rather than from quantitative units of measurement.
A table of norms and frequency distribution often provides percentile ranks. Or, if the percentile
ranks themselves are not given in a table, it is possible to calculate them easily from the frequency
distribution.
The percentile method is a technique whereby scores on two or more tests, given in units that are
different, may be transformed into uniform and comparable values. This method has the advantage
of not depending upon any assumptions regarding the characteristics of the distribution with
which it is used. The distribution might be normal, skewed, or rectangular. When a percentile
rank is given for a particular individual, it refers to his rank in the specified group of scores from
which it has been derived. On a test of reading comprehension at the fourth-grade level, for
example, a percentile rank of 60 for a particular pupil is relevant to the group of pupils for whom
the distribution of scores was found. Whether or not this same pupil would be rated at percentile
60 as a member of another fourth-grade population will depend on the comparability of the two
groups. His rating might be the same, or higher, or lower. (In this connection, consult, giving
norms for college freshmen.)

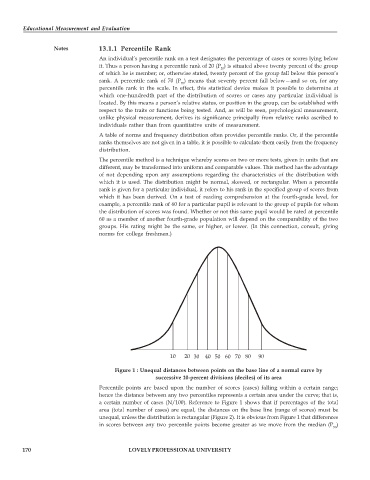
10 20 30 40 50 60 70 80 90

Figure 1 : Unequal distances between points on the base line of a normal curve by
successive 10-percent divisions (deciles) of its area
Percentile points are based upon the number of scores (cases) falling within a certain range;
hence the distance between any two percentiles represents a certain area under the curve; that is,
a certain number of cases (N/100). Reference to Figure 1 shows that if percentages of the total
area (total number of cases) are equal, the distances on the base line (range of scores) must be
unequal, unless the distribution is rectangular (Figure 2). It is obvious from Figure 1 that differences
in scores between any two percentile points become greater as we move from the median (P )
50

170 LOVELY PROFESSIONAL UNIVERSITY