Page 139 - DMTH401_REAL ANALYSIS

Unit 10: Limit of a Function

Similarly you see that values of f(x) approach 5 as x tends to 1 from the left i.e. through values Notes
smaller than 1. This leads us to define right hand and left hand limits as under:
Definition 2: Right Hand Limits and Left Hand Limits

Let a function f be defined in a neighbourhood of a point ‘a’ except possibly at ‘a’. It is said to tend
to a number A as x tends to a number ‘a’ from the right or through values greater than ‘a’ if given
a number  > 0, there exists a number  > 0 such that

|f(x) –A| <  for a <x < a + .
We write, it as
lim f(x) = A or lim f(x) = A or f(a+) = A.
-
-
x a+ x a 0
+
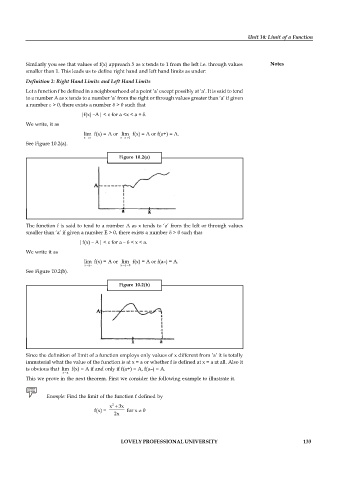
See Figure 10.2(a).
Figure 10.2(a)

The function f is said to tend to a number A as x tends to ‘a’ from the left or through values
smaller than ‘a’ if given a number E > 0, there exists a number  > 0 such that

|f(x) – A| <  for a – 6 < x < a.
We write it as
lim f(x) = A or lim f(x) = A or f(a–) = A.
-
-
-
x a– x a 0
See Figure 10.2(b).
Figure 10.2(b)

Since the definition of limit of a function employs only values of x different from ’a’ it is totally
immaterial what the value of the function is at x = a or whether f is defined at x = a at all. Also it
is obvious that lim f(x) = A if and only if f(a+) = A, f(a–) = A.
x a
-
This we prove in the next theorem. First we consider the following example to illustrate it.

Example: Find the limit of the function f defined by
2
x + 3x
f(x) = for x  0
2x

LOVELY PROFESSIONAL UNIVERSITY 133