Page 218 - DMTH401_REAL ANALYSIS

Real Analysis

Notes
+
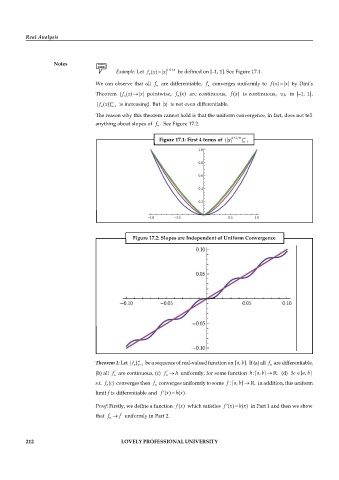
Example: Let f n ( ) = x 1 1/n be defined on [–1, 1]. See Figure 17.1.
x
We can observe that all f are differentiable, f converges uniformly to ( )f x = x by Dini’s
n
n
x
x
Theorem ( ( )f x ® x pointwise, f n ( ) are continuous, ( ) is continuous, " in [–1, 1],
f
x
n
x
{ ( )} ¥ n= 1 is increasing). But x is not even differentiable.
f
n
The reason why this theorem cannot hold is that the uniform convergence, in fact, does not tell
anything about slopes of f See Figure 17.2.
.
n
+
Figure 17.1: First 4 terms of { x 1 1/n ¥
}
n= 1

Figure 17.2: Slopes are Independent of Uniform Convergence

Theorem 1: Let { }f ¥ be a sequence of real-valued function on [ , ].a b If (a) all f are differentiable,
n n= 1 n
,
b
(b) all f are continuous, (c) f ® uniformly, for some function :[ , ]h a b ®  (d) c$ Î [ , ]
a
¢
¢
h
n n
f
a
,
b
s.t. f n ( ) converges then f converges uniformly to some :[ , ] ®  in addition, this uniform
c
n
=
x
x
limit f is differentiable and f ¢ ( ) h ( ).
Proof: Firstly, we define a function ( )f x which satisfies f ¢ ( ) h ( ) in Part 1 and then we show
x
x
=
that f ® f uniformly in Part 2.
n
212 LOVELY PROFESSIONAL UNIVERSITY