Page 249 - DMTH401_REAL ANALYSIS

Unit 20: The Riemann Integration

The lower (Riemann) sum off corresponding to the partition P, denoted by L(P, f), is defined by Notes
n
U(P,f) = å M  x . i
i
=
i 2
Before we pass on to the definition of upper and lower integrals, it is good for you to have the
geometrical meaning of the upper and lower sums and to visualize the above definitions
pictorially. You would, then, have a feeling for what is going on, and why such definitions are
made. Refer to Figure 20.4.
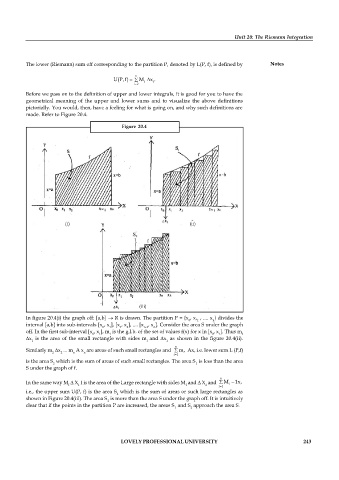
Figure 20.4

(i) (ii)

(iii)
In figure 20.4(i) the graph off: [a,b]  R is drawn. The partition P = {x , x, , .... x } divides the
0 1 n
interval [a,b] into sub-intervals [x , x ], [x , x ], .... [x , x ]. Consider the area S under the graph
0 1 1 2 n-1 n
off. In the first sub-interval [x , x ], m is the g.l.b. of the set of values f(x) for x in [x , x ]. Thus m
0 1 1 0 1 1
x is the area of the small rectangle with sides m and x as shown in the figure 20.4(ii).
1 l 1
n
Similarly m x ... m A x are areas of such small rectangles and å m, Ax, i.e. lower sum L (P,f)
2 2 n n
i 1
=
is the area S which is the sum of areas of such small rectangles. The area S is less than the area
2 1
S under the graph of f.
n
In the same way M  X I is the area of the Large rectangle with sides M and  X and å M - 1x,
i
I 1 I 1 i 1
=
i.e., the upper sum U(P, f) is the area S which is the sum of areas or such large rectangles as
2
shown in Figure 20.4(iii). The area S is more than the area S under the graph off. It is intuitively
2
clear that if the points in the partition P are increased, the areas S and S approach the area S.
1 2
LOVELY PROFESSIONAL UNIVERSITY 243