Page 247 - DMTH401_REAL ANALYSIS

Unit 20: The Riemann Integration

The total area enclosed by the graph of the function, X-axis and the ordinates x=a, x=b is equal to Notes
the sum of these areas i.e.
Area = A + A + A + A
1 2 3 4
= k d + k d + k d + k d .
1 1 2 2 3 3 4 4
Note that in the last equation, we have generalized the notion of area. In other words, we are
able to compute the area of a region which is not of rectangular shape. How did we get it? By
breaking up the region into a series of non-overlapping rectangles which include the totality of
the figure and summing up their respective areas. This is simply a slight obstraction of the same
process which is used in Geometry.
Since the graph of the function in figure 20.2 consists of 4 different steps, such a function, is called
a step function. What we have obtained is the area of a region bounded by
1. a non-negative step function
2. the vertical lines defined by x=a and x=b
3. the X-axis.

This area is just the sum of the areas of a finite number of f non-overlapping rectangles resulting
from the graph of the given function. The area is nothing but a real number.
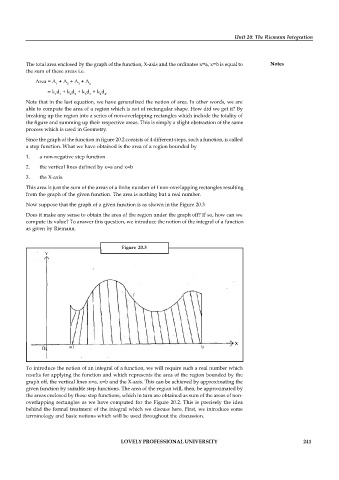
Now suppose that the graph of a given function is as shown in the Figure 20.3.

Does it make any sense to obtain the area of the region under the graph off? If so, how can we
compute its value? To answer this question, we introduce the notion of the integral of a function
as given by Riemann.

Figure 20.3

To introduce the notion of an integral of a function, we will require such a real number which
results for applying the function and which represents the area of the region bounded by the
graph off, the vertical lines x=a, x=b and the X-axis. This can be achieved by approximating the
given function by suitable step functions. The area of the region will, then, be approximated by
the areas enclosed by these step functions, which in turn are obtained as sum of the areas of non-
overlapping rectangles as we have computed for the Figure 20.2. This is precisely the idea
behind the formal treatment of the integral which we discuss here. First, we introduce some
terminology and basic notions which will be used throughout the discussion.

LOVELY PROFESSIONAL UNIVERSITY 241