Page 161 - DMTH402_COMPLEX_ANALYSIS_AND_DIFFERENTIAL_GEOMETRY

Complex Analysis and Differential Geometry

Notes
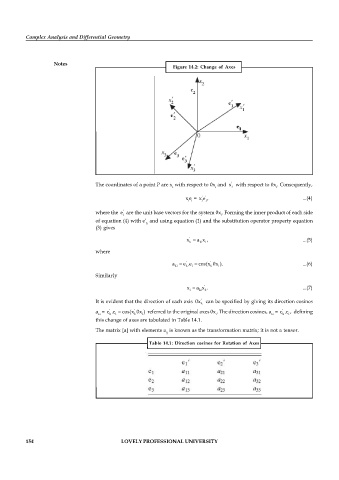
Figure 14.2: Change of Axes

'
The coordinates of a point P are x with respect to 0x and x with respect to 0x . Consequently,
i
i
i
i
'
x e = x e , ...(4)
'
i
j
i i
'
where the e are the unit base vectors for the system 0x . Forming the inner product of each side
i
i
of equation (4) with e’ and using equation (1) and the substitution operator property equation
k
(3) gives
'
x  a x , ...(5)
k
i
ki
where
'
'
a  e .e  cos(x 0x ). ...(6)
i
i
k
ki
k
Similarly
'
x  a x . ...(7)
ki
i
k
It is evident that the direction of each axis 0x can be specified by giving its direction cosines
'
k
'
'
'
a = e .e  cos(x 0x ) referred to the original axes 0x . The direction cosines, a = e .e , defining
k
i
i
k
i
k
ki
ki
i
this change of axes are tabulated in Table 14.1.
The matrix [a] with elements a is known as the transformation matrix; it is not a tensor.
ij
Table 14.1: Direction cosines for Rotation of Axes
154 LOVELY PROFESSIONAL UNIVERSITY