Page 255 - DMTH404_STATISTICS

Unit 17: System Reliability

Notes
Example 6: k-out-of-n System (n = 100,  = 1).

Uniform Exponential
k = 10 1.80 2.36
k = 50 1.01 0.71

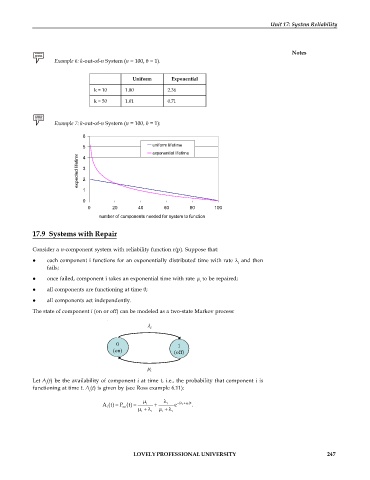
Example 7: k-out-of-n System (n = 100,  = 1):

6
5 4 uniform lifetime
expected lifetime 3 2
exponential lifetime

1
0
0 20 40 60 80 100
number of components needed for system to function

17.9 Systems with Repair

Consider a n-component system with reliability function r(p). Suppose that:
 each component i functions for an exponentially distributed time with rate  and then
i
fails;
 once failed, component i takes an exponential time with rate  to be repaired;
i
 all components are functioning at time 0;

 all components act independently.
The state of component i (on or off) can be modeled as a two-state Markov process:

 i

0 1
(on) (off)

 i
Let A (t) be the availability of component i at time t, i.e., the probability that component i is
i
functioning at time t. A (t) is given by (see Ross example 6.11):
i
 

A (t) P (t)  i  i e (  i   i )t .
oo
i
   i    i
i
i

LOVELY PROFESSIONAL UNIVERSITY 247