Page 327 - DMTH404_STATISTICS

Unit 23: Regression Analysis

The line of regression of Y on X, i.e Y = a + bX can also be written as Notes
i
Ci
Y =Y - bX +bX or Y - Y =b X - Xi .... (11)
d
i
Ci
Ci
i
s
or Y r Y X ) .... (12)
Y -
( Ci ) = × ( X -
i
s X
23.1.2 Line of Regression of X on Y
The general form of the line of regression of X on Y is X = c + dY , where X denotes the
Ci i Ci
predicted or calculated or estimated value of X for a given value of Y = Y and c and d are
i
constants. d is known as the regression coefficient of regression of X on Y.
In this case, we have to calculate the value of c and d so that
2
S' = (X - X ) is minimised.
i Ci
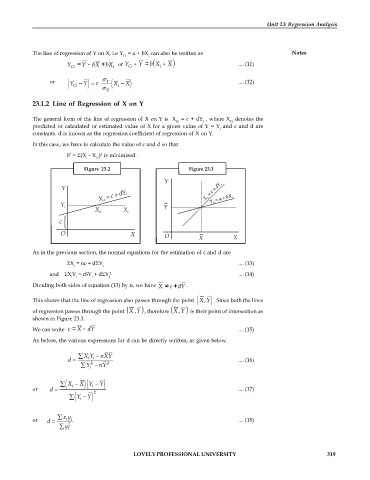
Figure 23.2 Figure 23.3

As in the previous section, the normal equations for the estimation of c and d are
X = nc + dY .... (13)
i i
and X Y = cSY + dY 2 .... (14)
i i i i
Dividing both sides of equation (13) by n, we have X = c +dY .

This shows that the line of regression also passes through the point ( X Y, ) . Since both the lines
d d
of regression passes through the point X ,Yi , therefore X ,Yi is their point of intersection as
shown in Figure 23.3.
We can write c = X - dY .... (15)

As before, the various expressions for d can be directly written, as given below.

å X Y - nXY
i i
d = 2 2 .... (16)
å Y - nY
i
å ( X - X Y - Y )
i
)( i
or d = 2 .... (17)
Y -
å ( i Y )
å x y
or d = i i .... (18)
å y 2 i

LOVELY PROFESSIONAL UNIVERSITY 319