Page 409 - DMTH404_STATISTICS

Unit 30: Method of Least Square

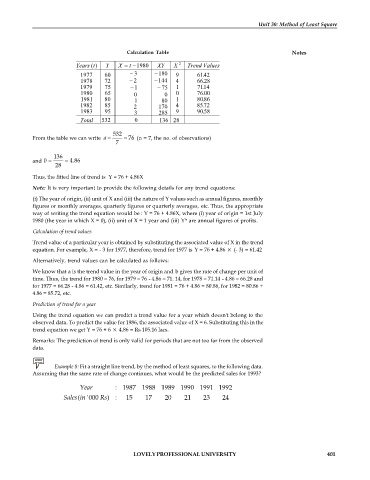
Calculation Table Notes

t
Years t) Y X = 1980 XY X 2 Trend Values
(
1977 60  3 180 9 61 .42
1978 72  2 144 4 66 .28
1979 75 1  75 1 71 .14
1980 65 0 0 0 76 .00
1981 80 1 80 1 80 .86
1982 85 2 170 4 85 .72
1983 95 3 285 9 90 .58
Total 532 0 136 28

532
From the table we can write a = = 76 (n = 7, the no. of observations)
7

136
and b = = 4.86
28
Thus, the fitted line of trend is Y = 76 + 4.86X
Note: It is very important to provide the following details for any trend equations:
(i) The year of origin, (ii) unit of X and (iii) the nature of Y values such as annual figures, monthly
figures or monthly averages, quarterly figures or quarterly averages, etc. Thus, the appropriate
way of writing the trend equation would be : Y = 76 + 4.86X, where (i) year of origin = 1st July
s
1980 (the year in which X = 0), (ii) unit of X = 1 year and (iii) Y' are annual figures of profits.
Calculation of trend values

Trend value of a particular year is obtained by substituting the associated value of X in the trend
equation. For example, X = - 3 for 1977, therefore, trend for 1977 is Y = 76 + 4.86  (- 3) = 61.42
Alternatively, trend values can be calculated as follows:

We know that a is the trend value in the year of origin and b gives the rate of change per unit of
time. Thus, the trend for 1980 = 76, for 1979 = 76 - 4.86 = 71. 14, for 1978 = 71.14 - 4.86 = 66.28 and
for 1977 = 66.28 - 4.86 = 61.42, etc. Similarly, trend for 1981 = 76 + 4.86 = 80.86, for 1982 = 80.86 +
4.86 = 85.72, etc.
Prediction of trend for a year
Using the trend equation we can predict a trend value for a year which doesn't belong to the
observed data. To predict the value for 1986, the associated value of X = 6. Substituting this in the
trend equation we get Y = 76 + 6  4.86 = Rs 105.16 lacs.
Remarks: The prediction of trend is only valid for periods that are not too far from the observed
data.

Example 8: Fit a straight line trend, by the method of least squares, to the following data.
Assuming that the same rate of change continues, what would be the predicted sales for 1993?
Year : 1987 1988 1989 1990 1991 1992
Sales (in '000 Rs ) : 15 17 20 21 23 24

LOVELY PROFESSIONAL UNIVERSITY 401