Page 383 - DMTH504_DIFFERENTIAL_AND_INTEGRAL_EQUATION

Differential and Integral Equation

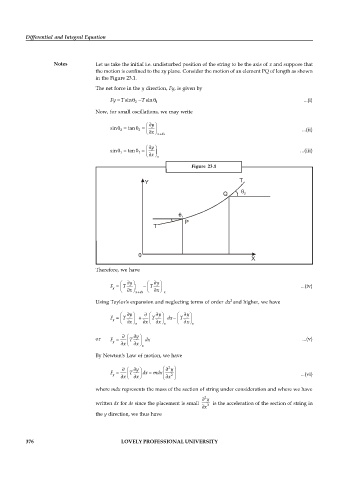
Notes Let us take the initial i.e. undisturbed position of the string to be the axis of x and suppose that
the motion is confined to the xy plane. Consider the motion of an element PQ of length as shown
in the Figure 23.1.
The net force in the y direction, Fy, is given by

Fy T sin T sin ...(i)
2 1
Now, for small oscillations, we may write

y
sin 2 tan 2 ...(ii)
x
x dx
y
sin 1 tan 1 ...(iii)
x x
Figure 23.1

Y T
Q 2

1
P
T

0
X
Therefore, we have

y y
F y T T ...(iv)
x x dx x x
2
Using Taylor s expansion and neglecting terms of order dx and higher, we have
y y y
F y T T dx T
x x x x
x x x
y
or F y T dx ...(v)
x x
x
By Newton s Law of motion, we have
y 2 y
F T dx mdx
y 2 ...(vi)
x x x
where mdx represents the mass of the section of string under consideration and where we have
2
y
written dx for ds since the placement is small 2 is the acceleration of the section of string in
x
the y direction, we thus have

376 LOVELY PROFESSIONAL UNIVERSITY