Page 195 - DSOC404_METHODOLOGY_OF_SOCIAL_RESEARCH_ENGLISH

Unit-27: Measures of Central Tendency: Mean, Median, Mode

= 1630 note
\ 6 × ∑x = 1630
Number of students (n) = 10
6 × ∑ x
formula of arithmetic average (M) =
n
6 × ∑ x 1630
M = = = 163
n 10
therefore, arithmetic mean (M) = 163 cm
(b) Short-cut Method—if the series is long and its values are different then it is difficult to
find the sum by direct method for calculating arithmetic average. Therefore, to reduce the effort and
time short-cut method is used. in this method any value is considered as mean, then deviation of
every value from this given supposed mean is calculated. in other words the difference between the
imagined mean and the values of elements is calculated separately. if the value of an element is less
than the imagined mean it is denoted by a negative sign (–) but if the value of an element is more
than the imagined mean it is denoted by a positive sign (+). in this way the deviation or difference of
every element is calculated then the sum of all the deviations is divided by the number of elements
and the value obtained from this is added to the supposed mean, this is real mean. this method can
be demonstrated with the help of given below example.

Example 2 Calculate the arithmetic average of 10 students given in example 1 with
the help of short-cutmethod.

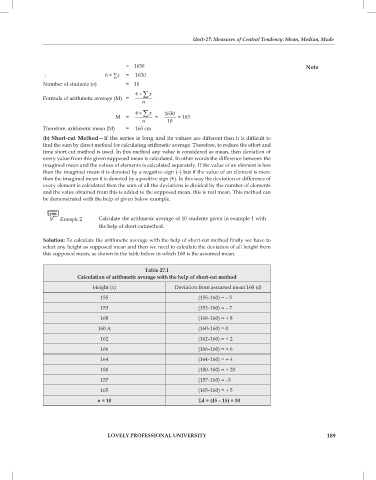
solution: To calculate the arithmetic average with the help of short-cut method firstly we have to
select any height as supposed mean and then we need to calculate the deviation of all height from
this supposed mean, as shown in the table below in which 160 is the assumed mean.

table 27.1
Calculation of arithmetic average with the help of short-cut method

Height (x) Deviation from assumed mean 160 (d)
155 (155–160) = – 5
153 (153–160) = – 7
168 (168–160) = + 8
160 A (160–160) = 0

162 (162–160) = + 2
166 (166–160) = + 6
164 (164–160) = + 4

180 (180–160) = + 20
157 (157–160) = –3
165 (165–160) = + 5
n = 10 Sd = (45 – 15) = 30

loVely professional uniVersity 189