Page 239 - DSOC404_METHODOLOGY_OF_SOCIAL_RESEARCH_ENGLISH

Unit–28: Measures of Dispersion: Standard Deviation

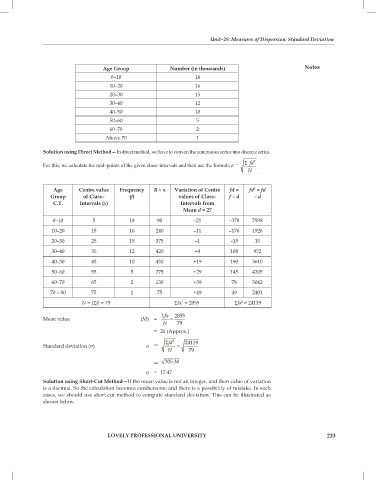
Age Group Number (in thousands) notes
0–10 18
10–20 16
20–30 15
30–40 12
40–50 10
50–60 5
60–70 2
Above 70 1

Solution using Direct Method—In direct method, we have to convert the continuous series into discrete series.

For this, we calculate the mid–points of the given class–intervals and then use the formula σ = S fd 2
N .

age centre value frequency B × x Variation of centre fd = fd = fd
2
Group of Class– (f) values of Class– f × d × d
c.t. intervals (x) intervals from
Mean d = 27
0–10 5 18 90 –21 –378 7938
10–20 15 16 240 –11 –176 1926

20–30 25 15 375 –1 –15 15
30–40 35 12 420 +9 108 972
40–50 45 10 450 +19 190 3610
50–60 55 5 275 +29 145 4205
60–70 65 2 130 +39 78 3042

70 – 80 75 1 75 +49 49 2401
N = (Sf) = 79 Sfx’ = 2055 Sfd = 24119
2
S fx 2055
Mean value (M) = = =
N 79
= 26 (Approx.)

standard deviation (s) σ = S fd 2 = 24119
N 79

= 305.30
σ = 17.47
Solution using Short-Cut Method—if the mean value is not an integer, and then value of variation
is a decimal. so the calculation becomes cumbersome and there is a possibility of mistake. in such
cases, we should use short-cut method to compute standard deviation. this can be illustrated as
shown below.

loVely professional uniVersity 233