Page 107 - DCOM303_DMGT504_OPERATION_RESEARCH
P. 107
Operations Research
Notes For Cochin, x + x + x = 2000
13 23 33
For Goa, x + x + x = 4000
14 24 34
The linear programming model for GM Textiles will be write in the next line. Minimize
Z = 5x + 6x + 9x + 7x + 7x + 8x + 2x + 4x + 6x + 3x + 5x + 3x
11 12 13 14 21 22 23 24 31 32 33 34
Subject to constraints,
X +x +x +x 6000 (i)
11 12 13 14
X +x +x +x 5000 (ii)
21 22 23 24
X +x +x +x 4000 (iii)
31 32 33 34
X +x +x = 5000 (iv)
11 21 31
X +x +x = 4000 (v)
12 22 32
X +x +x = 2000 (vi)
13 23 33
X +x +x = 4000 (vii)
14 24 34
Where, x 0 for i = 1, 2, 3 and j = 1, 2, 3, 4.
ij
Example: Consider the following transportation problem (Table 3.3) and develop a
linear programming (LP) model.
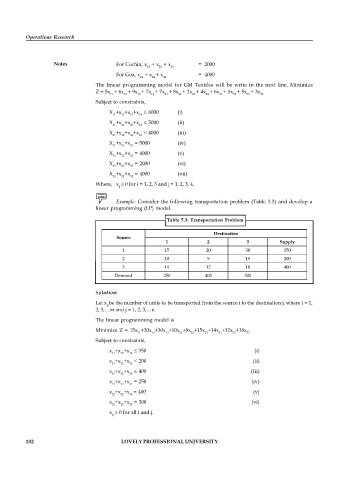
Table 5.3: Transportation Problem
Destination
Source
1 2 3 Supply
1 15 20 30 350
2 10 9 15 200
3 14 12 18 400
Demand 250 400 300
Solution:
Let x be the number of units to be transported from the source i to the destination j, where i = 1,
ij
2, 3,…m and j = 1, 2, 3,…n.
The linear programming model is
Minimize Z = 15x +20x +30x +10x +9x +15x +14x +12x +18x
11 12 13 21 22 23 31 32 33
Subject to constraints,
x +x +x 350 (i)
11 12 13
x +x +x 200 (ii)
21 22 23
x +x +x 400 (iii)
31 32 33
x +x +x = 250 (iv)
11 12 31
x +x +x = 400 (v)
12 22 32
x +x +x = 300 (vi)
13 23 33
x 0 for all i and j.
ij
102 LOVELY PROFESSIONAL UNIVERSITY