Page 108 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 5: Transportation Problem

In the above LP problem, there are m x n = 3 x 3 = 9 decision variables and Notes
m + n = 3 + 3 = 6 constraints.

5.4 Maximization Transportation Problem

In this type of problem, the objective is to maximize the total profit or return. In this case,
convert the maximization problem into minimization by subtracting all the unit cost from the
highest unit cost given in the table and solve.

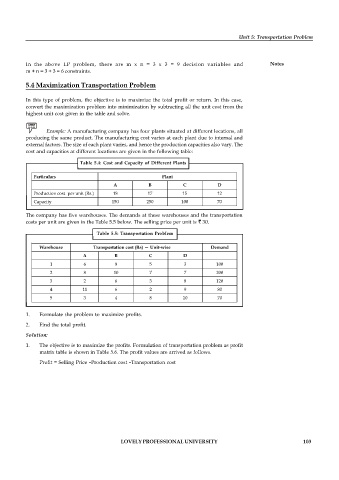
Example: A manufacturing company has four plants situated at different locations, all
producing the same product. The manufacturing cost varies at each plant due to internal and
external factors. The size of each plant varies, and hence the production capacities also vary. The
cost and capacities at different locations are given in the following table:
Table 5.4: Cost and Capacity of Different Plants

Particulars Plant
A B C D
Production cost per unit (Rs.) 18 17 15 12
Capacity 150 250 100 70

The company has five warehouses. The demands at these warehouses and the transportation
costs per unit are given in the Table 5.5 below. The selling price per unit is ` 30.

Table 5.5: Transportation Problem

Warehouse Transportation cost (Rs) — Unit-wise Demand
A B C D
1 6 9 5 3 100
2 8 10 7 7 200
3 2 6 3 8 120
4 11 6 2 9 80
5 3 4 8 10 70

1. Formulate the problem to maximize profits.

2. Find the total profit.
Solution:
1. The objective is to maximize the profits. Formulation of transportation problem as profit
matrix table is shown in Table 5.6. The profit values are arrived as follows.
Profit = Selling Price –Production cost –Transportation cost

LOVELY PROFESSIONAL UNIVERSITY 103