Page 96 - DCOM303_DMGT504_OPERATION_RESEARCH

Unit 4: Linear Programming – Duality

Notes
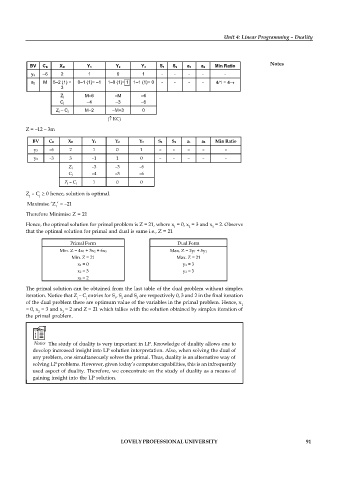
BV C B X B Y 1 Y 2 Y 3 S 1 S 2 a 1 a 2 Min Ratio
y 3 –6 2 1 0 1 - - - - -
a 2 M 5–2 (1) = 0–1 (1)= –1 1–0 (1)= 1 1–1 (1)= 0 - - - - 4/1 = 4
3
Z j M–6 –M –6
C j –4 –3 –6
Z j – C j M–2 –M+3 0
( KC)
Z = –12 – 3m
BV CB XB Y1 Y2 Y3 S1 S2 a1 a2 Min Ratio
y3 –6 2 1 0 1 – – – – –
y2 –3 3 –1 1 0 – – – – –
Zj –3 –3 –6
Cj –4 –3 –6
Zj – Cj 1 0 0

Z – C  0 hence, solution is optimal.
J J
Maximise ‘Z ’ = –21
1
Therefore Minimise Z = 21

Hence, the optimal solution for primal problem is Z = 21, where x = 0, x = 3 and x = 2. Observe
1 2 3
that the optimal solution for primal and dual is same i.e., Z = 21
Primal Form Dual Form
Min. Z = 4x1 + 3x2 + 6x3 Max. Z = 2y1 + 5y2
Min. Z = 21 Max. Z = 21
x1 = 0 y1 = 3
x2 = 3 y2 = 3
x3 = 2

The primal solution can be obtained from the last table of the dual problem without simplex
iteration. Notice that Z – C entries for S , S and S are respectively 0, 3 and 2 in the final iteration
j j 1 2 3
of the dual problem there are optimum value of the variables in the primal problem. Hence, x
1
= 0, x = 3 and x = 2 and Z = 21 which tallies with the solution obtained by simplex iteration of
2 3
the primal problem.

Notes The study of duality is very important in LP. Knowledge of duality allows one to
develop increased insight into LP solution interpretation. Also, when solving the dual of
any problem, one simultaneously solves the primal. Thus, duality is an alternative way of
solving LP problems. However, given today’s computer capabilities, this is an infrequently
used aspect of duality. Therefore, we concentrate on the study of duality as a means of
gaining insight into the LP solution.

LOVELY PROFESSIONAL UNIVERSITY 91