Page 96 - DCOM504_SECURITY_ANALYSIS_AND_PORTFOLIO_MANAGEMENT

Unit 2: Risk and Return

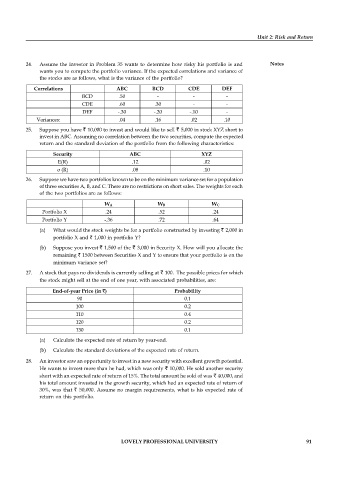
24. Assume the investor in Problem 35 wants to determine how risky his portfolio is and Notes
wants you to compute the portfolio variance. If the expected correlations and variance of
the stocks are as follows, what is the variance of the portfolio?
Correlations ABC BCD CDE DEF
BCD .50 - - -
CDE .60 .30 - -
DEF -.30 -.20 -.10 -
Variances: .04 .16 .02 .10

25. Suppose you have 10,000 to invest and would like to sell 5,000 in stock XYZ short to
invest in ABC. Assuming no correlation between the two securities, compute the expected
return and the standard deviation of the portfolio from the following characteristics:
Security ABC XYZ
E(R) .12 .02
σ (R) .08 .10

26. Suppose we have two portfolios known to be on the minimum variance set for a population
of three securities A, B, and C. There are no restrictions on short sales. The weights for each
of the two portfolios are as follows:
W A W B W C
Portfolio X .24 .52 .24
Portfolio Y -.36 .72 .64
(a) What would the stock weights be for a portfolio constructed by investing 2,000 in

portfolio X and 1,000 in portfolio Y?
(b) Suppose you invest 1,500 of the 3,000 in Security X. How will you allocate the
remaining 1500 between Securities X and Y to ensure that your portfolio is on the
minimum variance set?
27. A stock that pays no dividends is currently selling at 100. The possible prices for which
the stock might sell at the end of one year, with associated probabilities, are:
End-of-year Price (in ) Probability
90 0.1
100 0.2
110 0.4
120 0.2
130 0.1
(a) Calculate the expected rate of return by year-end.
(b) Calculate the standard deviations of the expected rate of return.

28. An investor saw an opportunity to invest in a new security with excellent growth potential.
He wants to invest more than he had, which was only 10,000. He sold another security
short with an expected rate of return of 15%. The total amount he sold of was 40,000, and
his total amount invested in the growth security, which had an expected rate of return of
30%, was that 50,000. Assume no margin requirements, what is his expected rate of
return on this portfolio.

LOVELY PROFESSIONAL UNIVERSITY 91