Page 144 - DCAP310_INTRODUCTION_TO_ARTIFICIAL_INTELLIGENCE_AND_EXPERT_SYSTEMS

Introduction to Artificial Intelligence & Expert Systems

Notes “Dead” are each subsets of “Either”. The “Alive” plausibility is 1 – m (Dead) and the “Dead”
plausibility is 1 – m (Alive). Finally, the “Either” plausibility sums m(Alive) + m(Dead) +
m(Either). The universal hypothesis (“Either”) will always have 100% belief and plausibility—
it acts as a checksum of sorts.
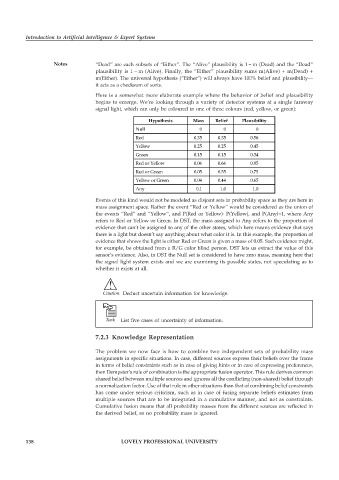
Here is a somewhat more elaborate example where the behavior of belief and plausibility
begins to emerge. We’re looking through a variety of detector systems at a single faraway
signal light, which can only be coloured in one of three colours (red, yellow, or green):

Hypothesis Mass Belief Plausibility
Null 0 0 0
Red 0.35 0.35 0.56
Yellow 0.25 0.25 0.45
Green 0.15 0.15 0.34
Red or Yellow 0.06 0.66 0.85
Red or Green 0.05 0.55 0.75
Yellow or Green 0.04 0.44 0.65
Any 0.1 1.0 1.0
Events of this kind would not be modeled as disjoint sets in probability space as they are here in
mass assignment space. Rather the event “Red or Yellow” would be considered as the union of
the events “Red” and “Yellow”, and P(Red or Yellow)· P(Yellow), and P(Any)=1, where Any
refers to Red or Yellow or Green. In DST, the mass assigned to Any refers to the proportion of
evidence that can’t be assigned to any of the other states, which here means evidence that says
there is a light but doesn’t say anything about what color it is. In this example, the proportion of
evidence that shows the light is either Red or Green is given a mass of 0.05. Such evidence might,
for example, be obtained from a R/G color blind person. DST lets us extract the value of this
sensor’s evidence. Also, in DST the Null set is considered to have zero mass, meaning here that
the signal light system exists and we are examining its possible states, not speculating as to
whether it exists at all.

!
Caution Deduct uncertain information for knowledge.

Task List five cases of uncertainty of information.

7.2.3 Knowledge Representation

The problem we now face is how to combine two independent sets of probability mass
assignments in specific situations. In case, different sources express their beliefs over the frame
in terms of belief constraints such as in case of giving hints or in case of expressing preferences,
then Dempster’s rule of combination is the appropriate fusion operator. This rule derives common
shared belief between multiple sources and ignores all the conflicting (non-shared) belief through
a normalization factor. Use of that rule in other situations than that of combining belief constraints
has come under serious criticism, such as in case of fusing separate beliefs estimates from
multiple sources that are to be integrated in a cumulative manner, and not as constraints.
Cumulative fusion means that all probability masses from the different sources are reflected in
the derived belief, so no probability mass is ignored.

138 LOVELY PROFESSIONAL UNIVERSITY