Page 127 - DCAP313_LAB_ON_COMPUTER_GRAPHICS

Unit 8: Implementing of Scaling in 2D Transformation

We can also write points in vector/matrix notation as Notes
x È ˘
p = Í ˙
y
Î ˚
8.1.1 Translations
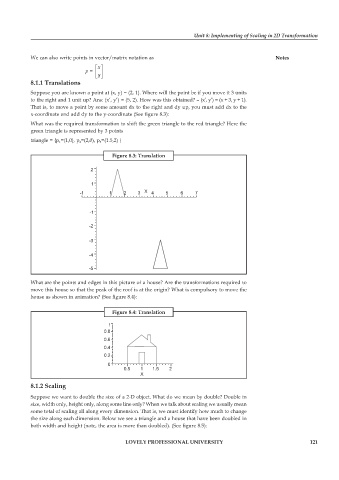
Suppose you are known a point at (x, y) = (2, 1). Where will the point be if you move it 3 units
to the right and 1 unit up? Ans: (x’, y’) = (5, 2). How was this obtained? – (x’, y’) = (x + 3, y + 1).
That is, to move a point by some amount dx to the right and dy up, you must add dx to the
x-coordinate and add dy to the y-coordinate (See figure 8.3):
What was the required transformation to shift the green triangle to the red triangle? Here the
green triangle is represented by 3 points
triangle = {p 1 =(1,0), p 2 =(2,0), p 3 =(1.5,2) }

Figure 8.3: Translation

What are the points and edges in this picture of a house? Are the transformations required to
move this house so that the peak of the roof is at the origin? What is compulsory to move the
house as shown in animation? (See figure 8.4):

Figure 8.4: Translation

8.1.2 Scaling
Suppose we want to double the size of a 2-D object. What do we mean by double? Double in
size, width only, height only, along some line only? When we talk about scaling we usually mean
some total of scaling all along every dimension. That is, we must identify how much to change
the size along each dimension. Below we see a triangle and a house that have been doubled in
both width and height (note, the area is more than doubled). (See figure 8.5):

LOVELY PROFESSIONAL UNIVERSITY 121