Page 128 - DCAP313_LAB_ON_COMPUTER_GRAPHICS

Lab on Computer Graphics

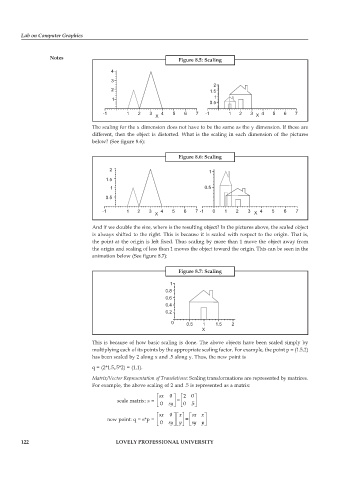
Notes Figure 8.5: Scaling

The scaling for the x dimension does not have to be the same as the y dimension. If these are
different, then the object is distorted. What is the scaling in each dimension of the pictures
below? (See figure 8.6):

Figure 8.6: Scaling

And if we double the size, where is the resulting object? In the pictures above, the scaled object
is always shifted to the right. This is because it is scaled with respect to the origin. That is,
the point at the origin is left fixed. Thus scaling by more than 1 move the object away from
the origin and scaling of less than 1 moves the object toward the origin. This can be seen in the
animation below (See figure 8.7):

Figure 8.7: Scaling

This is because of how basic scaling is done. The above objects have been scaled simply by
multiplying each of its points by the appropriate scaling factor. For example, the point p = (1.5,2)
has been scaled by 2 along x and .5 along y. Thus, the new point is

q = (2*1.5,.5*2) = (1,1).
Matrix/Vector Representation of Translations: Scaling transformations are represented by matrices.
For example, the above scaling of 2 and .5 is represented as a matrix:
È sx 0 ˘ 2 È 0 ˘
scale matrix: s = Í ˙ = Í ˙
Î 0 sy ˚ Î 0 . 5 ˚
È sx 0 ˘ x È ˘ È sx x˘
new point: q = s*p = Í ˙ Í ˙ = Í ˙
y
Î 0 sy ˚ Î ˚ Î sy y ˚

122 LOVELY PROFESSIONAL UNIVERSITY