Page 132 - DMTH201_Basic Mathematics-1

Unit 5: Equations of Straight Lines

5.2.1 Slope of a Line when Coordinates of any Two Points on the Line Notes
are given

We know that a line is completely determined when we are given two points on it. Hence, we
proceed to find the slope of a line in terms of the coordinates of two points on the line.
The slope of a line (also called the gradient of a line) is a number that describes how "steep" it is.
If the line slopes downwards to the right, it has a negative slope. As x increases, y decreases. If
the line sloped upwards to the right, the slope would be a positive number. Adjust the points
above to create a positive slope. The slope of a line can positive, negative, zero or undefined.
Let P(x , y ) and Q(x , y ) be two points on non-vertical line lwhose inclination is . Obviously,
1 1 2 2
x x , otherwise the line will become perpendicular to x-axis and its slope will not be defined.
1 2
The inclination of the line l may be acute or obtuse. Let us take these two cases.
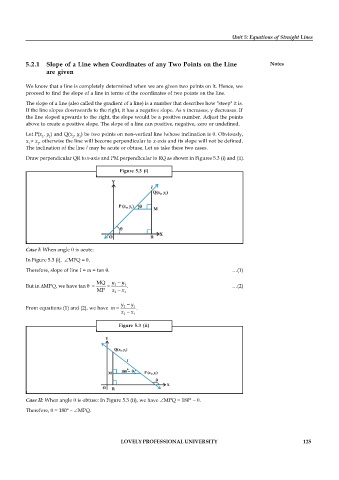
Draw perpendicular QR to x-axis and PM perpendicular to RQ as shown in Figures 5.3 (i) and (ii).

Figure 5.3 (i)

Case I: When angle is acute:
In Figure 5.3 (i), MPQ = .

Therefore, slope of line l = m = tan . …(1)

MQ y y
But in MPQ, we have tan 2 1 . …(2)
MP x x
2 1
y y
From equations (1) and (2), we have m 2 1 .
x 2 x 1

Figure 5.3 (ii)

Case II: When angle is obtuse: In Figure 5.3 (ii), we have MPQ = 180° .

Therefore, = 180° MPQ.

LOVELY PROFESSIONAL UNIVERSITY 125