Page 163 - DMTH201_Basic Mathematics-1

Basic Mathematics – I

Notes

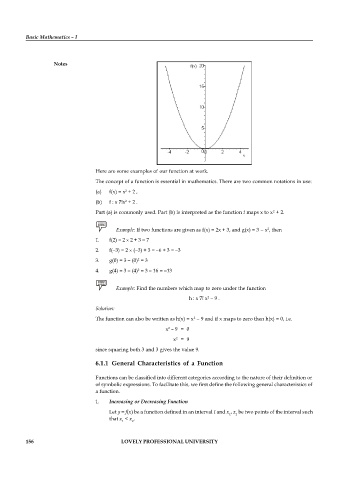
Here are some examples of our function at work.
The concept of a function is essential in mathematics. There are two common notations in use:

2
(a) f(x) = x + 2 ,
2
(b) f : x 7!x + 2 .
2
Part (a) is commonly used. Part (b) is interpreted as the function f maps x to x + 2.

2
Example: If two functions are given as f(x) = 2x + 3, and g(x) = 3 x , then
1. f(2) = 2 2 + 3 = 7
2. f( 3) = 2 ( 3) + 3 = 6 + 3 = 3

3. g(0) = 3 (0) = 3
2
4. g(4) = 3 (4) = 3 16 = 13
2

Example: Find the numbers which map to zero under the function
2
h : x 7! x 9 .
Solution:
The function can also be written as h(x) = x 9 and if x maps to zero then h(x) = 0, i.e.
2
x – 9 = 0
2
x = 9
2
since squaring both 3 and 3 gives the value 9.

6.1.1 General Characteristics of a Function

Functions can be classified into different categories according to the nature of their definition or
of symbolic expressions. To facilitate this, we first define the following general characteristics of
a function.

1. Increasing or Decreasing Function
Let y = f(x) be a function defined in an interval I and x , x be two points of the interval such
1 2
that x < x .
1 2

156 LOVELY PROFESSIONAL UNIVERSITY