Page 136 - DMTH201_Basic Mathematics-1

Unit 5: Equations of Straight Lines

Notes
1
Let m 1 ,m 2 m and .
2 4
Now, putting these values in (1), we get

1 1
m m
tan = 2 or 1 2 ,
4 1 1 m 1 1 m
2 2

1 1
m m
which gives 2 = 1 or 2 1.
1 1
1 m 1 m
2 2
1
Therefore m = 3 or m .
3

1
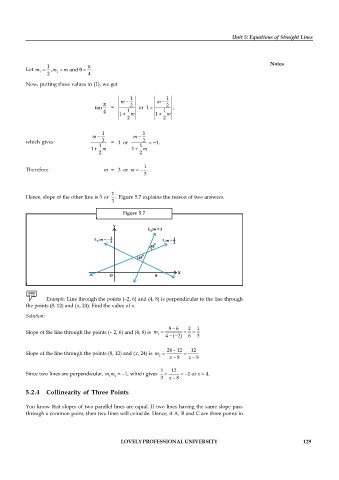
Hence, slope of the other line is 3 or . Figure 5.7 explains the reason of two answers.
3
Figure 5.7

Example: Line through the points (–2, 6) and (4, 8) is perpendicular to the line through
the points (8, 12) and (x, 24). Find the value of x.

Solution:

8 6 2 1
Slope of the line through the points (– 2, 6) and (4, 8) is m 1
4 ( 2) 6 3
24 12 12
Slope of the line through the points (8, 12) and (x, 24) is m 2
x 8 x 8

1 12
Since two lines are perpendicular, m m = 1, which gives 1 or x 4.
1 2
3 x 8
5.2.4 Collinearity of Three Points

You know that slopes of two parallel lines are equal. If two lines having the same slope pass
through a common point, then two lines will coincide. Hence, if A, B and C are three points in

LOVELY PROFESSIONAL UNIVERSITY 129